题目内容
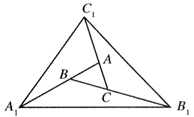
对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A 、B
、B 、C
、C ,使得A
,使得A B=2AB,B
B=2AB,B C=2BC,C
C=2BC,C A=2CA,顺次连接A
A=2CA,顺次连接A 、B
、B 、C
、C ,得到△A
,得到△A B
B C
C (如图所示),记其面积为S
(如图所示),记其面积为S .现再分别延长A
.现再分别延长A B
B 、B
、B C
C 、C
、C A
A 至点A
至点A 、B
、B 、C
、C ,使得A
,使得A B
B =2A
=2A B
B ,B
,B C
C =2B
=2B C
C ,C
,C A
A =2C
=2C A
A ,顺次连接A
,顺次连接A 、B
、B 、C
、C ,得到△A
,得到△A B
B C
C ,记其面积为S
,记其面积为S ,则S
,则S =_____________.
=_____________.
 、B
、B 、C
、C ,使得A
,使得A B=2AB,B
B=2AB,B C=2BC,C
C=2BC,C A=2CA,顺次连接A
A=2CA,顺次连接A 、B
、B 、C
、C ,得到△A
,得到△A B
B C
C (如图所示),记其面积为S
(如图所示),记其面积为S .现再分别延长A
.现再分别延长A B
B 、B
、B C
C 、C
、C A
A 至点A
至点A 、B
、B 、C
、C ,使得A
,使得A B
B =2A
=2A B
B ,B
,B C
C =2B
=2B C
C ,C
,C A
A =2C
=2C A
A ,顺次连接A
,顺次连接A 、B
、B 、C
、C ,得到△A
,得到△A B
B C
C ,记其面积为S
,记其面积为S ,则S
,则S =_____________.
=_____________.
361
试题分析:连接A1C,找出延长各边后得到的三角形是原三角形的19倍的规律,利用规律求解即可.
解:连接A1C

S△AA1C=3S△ABC=3,
S△AA1C1=2S△AA1C=6,
所以S△A1B1C1=6×3+1=19;
则可得S△A2B2C2=19×19=361,即S
 =361.
=361.点评:解答此类问题的关键是仔细分析所给图形的特征得到规律,再把得到的规律应用于解题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
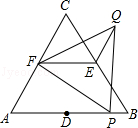
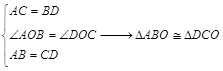
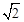 ≤r<2时,S的取值范围是 .
≤r<2时,S的取值范围是 .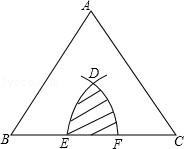
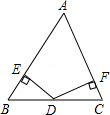
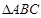 中,
中,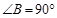 ,若按图中虚线剪去
,若按图中虚线剪去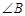 ,则
,则 等于( )
等于( )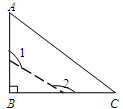
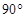
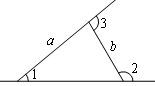
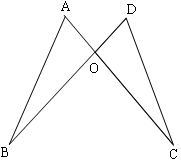
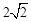 ,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .
,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .