Question

如图，在直角坐标系中，A、B是某一次函数图象上的两点，满足∠AOB是直角，且AO=BO=2，若AO与y轴的夹角是60°，求这个一次函数．

Answer 1

解：如图，作AC⊥CE，BE⊥CE，
∵AO与y轴的夹角是60°，即∠AOF=60°，
∴∠AOC=30°，
∵∠AOB是直角，∠FOE是直角，
∴∠BOE=60°，
∴∠OBE=30°，
又∵AO=BO=2，
∴AC=1，OE=1，
∴C0=，BE=，
∴点A（-，1），点B（1，），
设一次函数的解析式为y=kx+b，
把A、B两点代入得，
，
解得，，
∴一次函数关系式是y=（）x+．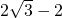
分析：作AC⊥CE，BE⊥CE，根据题意，可得∠AOC=30°，∠OBE=30°，根据直角三角形的边角关系，可得出AC、OC和0E、BE的长，即得点A、点B的坐标，用待定系数法，求出一次函数的解析式即可．
点评：本题主要考查了一次函数的应用，用待定系数法，求一次函数的解析式，得出点的坐标是解答的关键．