题目内容
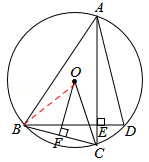
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,求证:

(1)△AEB∽△OFC;
(2)AD=2FO.

(1)△AEB∽△OFC;
(2)AD=2FO.
证明:(1)如图,连接OB,则∠BAE=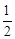 ∠BOC,
∠BOC,
∵OF⊥BC,∴∠COF=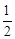 ∠BOC。
∠BOC。
∴∠BAE=∠COF。
又∵AC⊥BD,OF⊥BC,∴∠OFC=∠AEB=90°。
∴△AEB∽△OFC。
(2)∵△AEB∽△OFC,∴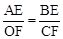 ,即
,即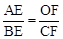 。
。
由圆周角定理,∠D=∠BCE,∠DAE=∠CBE,
∴△ADE∽△BCE。∴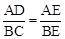 。
。
∴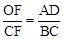 。
。
∵OF⊥BC,∴BC=2CF。
∴AD =2FO。
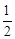 ∠BOC,
∠BOC,
∵OF⊥BC,∴∠COF=
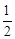 ∠BOC。
∠BOC。∴∠BAE=∠COF。
又∵AC⊥BD,OF⊥BC,∴∠OFC=∠AEB=90°。
∴△AEB∽△OFC。
(2)∵△AEB∽△OFC,∴
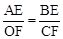 ,即
,即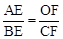 。
。由圆周角定理,∠D=∠BCE,∠DAE=∠CBE,
∴△ADE∽△BCE。∴
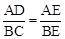 。
。∴
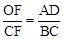 。
。∵OF⊥BC,∴BC=2CF。
∴AD =2FO。
试题分析:(1)连接OB,根据圆周角定理可得∠BAE=
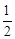 ∠BOC,根据垂径定理可得∠COF=
∠BOC,根据垂径定理可得∠COF=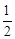 ∠BOC,再根据垂直的定义可得∠OFC=∠AEB=90°,然后根据两角对应相等,两三角形相似证明即可;
∠BOC,再根据垂直的定义可得∠OFC=∠AEB=90°,然后根据两角对应相等,两三角形相似证明即可;(2)根据相似三角形对应边成比例可得
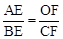 ,再根据圆周角定理求出∠D=∠BCE,∠DAE=∠CBE,然后求出△ADE和△BCE相似,根据相似三角形对应边成比例可得
,再根据圆周角定理求出∠D=∠BCE,∠DAE=∠CBE,然后求出△ADE和△BCE相似,根据相似三角形对应边成比例可得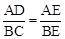 ,从而得到
,从而得到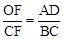 ,再根据垂径定理BC=2FC,代入整理即可得证。
,再根据垂径定理BC=2FC,代入整理即可得证。 
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目







 ,求EF的长.
,求EF的长.