题目内容
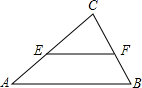 如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A,C不重合)在AC边上,EF∥AB交BC于F点.
如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A,C不重合)在AC边上,EF∥AB交BC于F点.
(1)当△ECF的面积与四边形EABF的面积相等时,求CE的长;
(2)当△ECF的周长与四边形EABF的周长相等时,求CE的长;
(3)试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF的长.
解:(1)∵△ECF的面积与四边形EABF的面积相等
∴S△ECF:S△ACB=1:2
又∵EF∥AB∴△ECF∽△ACB
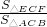 =
=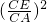 =
=
∵AC=4,
∴CE= ;
;
(2)设CE的长为x
∵△ECF∽△ACB
∴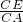 =
=
∴CF=
由△ECF的周长与四边形EABF的周长相等,
得x+EF+ x=(4-x)+5+(3-
x=(4-x)+5+(3- x)+EF
x)+EF
解得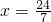
∴CE的长为 ;
;
(3)△EFP为等腰直角三角形,有两种情况: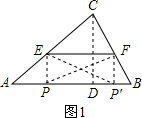
①如图1,假设∠PEF=90°,EP=EF
由AB=5,BC=3,AC=4,得∠C=90°
∴Rt△ACB斜边AB上高CD=
设EP=EF=x,由△ECF∽△ACB,得:
 =
=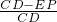
即 =
=
解得x= ,即EF=
,即EF=
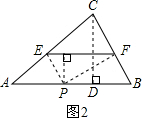
当∠EFP?=90°,EF=FP′时,同理可得EF= ;
;
②如图2,假设∠EPF=90°,PE=PF时,点P到EF的距离为 EF
EF
设EF=x,由△ECF∽△ACB,得:
 =
=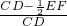 ,即
,即 =
=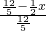
解得x=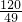 ,即EF=
,即EF=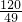
综上所述,在AB上存在点P,使△EFP为等腰直角三角形,此时EF= 或EF=
或EF=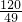 .
.
分析:(1)因为EF∥AB,所以容易想到用相似三角形的面积比等于相似比的平方解题;
(2)根据周长相等,建立等量关系,列方程解答;
(3)先画出图形,根据图形猜想P点可能的位置,再找到相似三角形,依据相似三角形的性质解答.
点评:此题考查了相似三角形的性质,有一定的开放性,难点在于作出辅助线就具体情况进行分类讨论.
∴S△ECF:S△ACB=1:2
又∵EF∥AB∴△ECF∽△ACB
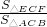 =
=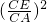 =
=
∵AC=4,
∴CE=
 ;
;(2)设CE的长为x
∵△ECF∽△ACB
∴
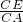 =
=
∴CF=

由△ECF的周长与四边形EABF的周长相等,
得x+EF+
 x=(4-x)+5+(3-
x=(4-x)+5+(3- x)+EF
x)+EF解得
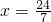
∴CE的长为
 ;
;(3)△EFP为等腰直角三角形,有两种情况:

①如图1,假设∠PEF=90°,EP=EF
由AB=5,BC=3,AC=4,得∠C=90°
∴Rt△ACB斜边AB上高CD=

设EP=EF=x,由△ECF∽△ACB,得:
 =
=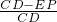
即
 =
=
解得x=
 ,即EF=
,即EF=

当∠EFP?=90°,EF=FP′时,同理可得EF=
 ;
;②如图2,假设∠EPF=90°,PE=PF时,点P到EF的距离为
 EF
EF设EF=x,由△ECF∽△ACB,得:
 =
=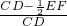 ,即
,即 =
=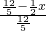
解得x=
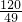 ,即EF=
,即EF=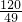
综上所述,在AB上存在点P,使△EFP为等腰直角三角形,此时EF=
 或EF=
或EF=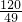 .
.分析:(1)因为EF∥AB,所以容易想到用相似三角形的面积比等于相似比的平方解题;
(2)根据周长相等,建立等量关系,列方程解答;
(3)先画出图形,根据图形猜想P点可能的位置,再找到相似三角形,依据相似三角形的性质解答.
点评:此题考查了相似三角形的性质,有一定的开放性,难点在于作出辅助线就具体情况进行分类讨论.

练习册系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=