题目内容
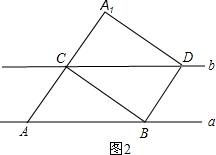
如图1,若四边形ABCD、四边形GFED都是正方形,显然图中有AG=CE,AG⊥CE;(1)当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明;若不成立,请说明理由;
(2)当正方形GFED绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.
①求证:AG⊥CH;
②当AD=4,DG=
| 2 |

分析:(1)寻找AG、CE所在的两个三角形全等的条件,证明全等即可;
(2)①由△AGD≌△CED,可知∠1=∠2,利用对顶角相等及互余关系证明垂直;
②连接GE交AD于P,根据S△AGD+S△ACD=S四边形ACDG=S△ACG+S△CGD,再分别表示四个三角形的底和高,列方程求CH.
(2)①由△AGD≌△CED,可知∠1=∠2,利用对顶角相等及互余关系证明垂直;
②连接GE交AD于P,根据S△AGD+S△ACD=S四边形ACDG=S△ACG+S△CGD,再分别表示四个三角形的底和高,列方程求CH.
解答: 解:(1)AG=CE成立.
解:(1)AG=CE成立.
证明:∵四边形ABCD、四边形DEFG是正方形,
∴GD=DE,AD=DC,(1分)
∠GDE=∠ADC=90°.
∴∠GDA=90°-∠ADE=∠EDC. (2分)
∴△AGD≌△CED.
∴AG=CE. (3分)
 (2)①类似(1)可得△AGD≌△CED,
(2)①类似(1)可得△AGD≌△CED,
∴∠1=∠2. (4分)
又∵∠HMA=∠DMC,
∴∠AHM=∠ADC=90°,
即AG⊥CH. (5分)
②连接GE,交AD于P,连接CG,
由题意有GP=PD=
×sin45°=1,
∴AP=3,AG=
. (8分)
∵EG⊥AD,CD⊥AD,∴EG∥CD,
∴以CD为底边的△CDG的高为PD=1,(延长CD画高)
S△AGD+S△ACD=S四边形ACDG=S△ACG+S△CGD
∴4×1+4×4=
×CH+4×1
∴CH=
. (10分)
 解:(1)AG=CE成立.
解:(1)AG=CE成立.证明:∵四边形ABCD、四边形DEFG是正方形,
∴GD=DE,AD=DC,(1分)
∠GDE=∠ADC=90°.
∴∠GDA=90°-∠ADE=∠EDC. (2分)
∴△AGD≌△CED.
∴AG=CE. (3分)
 (2)①类似(1)可得△AGD≌△CED,
(2)①类似(1)可得△AGD≌△CED,∴∠1=∠2. (4分)
又∵∠HMA=∠DMC,
∴∠AHM=∠ADC=90°,
即AG⊥CH. (5分)
②连接GE,交AD于P,连接CG,
由题意有GP=PD=
| 2 |
∴AP=3,AG=
| 10 |
∵EG⊥AD,CD⊥AD,∴EG∥CD,
∴以CD为底边的△CDG的高为PD=1,(延长CD画高)
S△AGD+S△ACD=S四边形ACDG=S△ACG+S△CGD
∴4×1+4×4=
| 10 |
∴CH=
8
| ||
| 5 |
点评:本题综合性较强,考查了三角形全等、相似的判定及性质,解直角三角形,勾股定理等相关知识.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目