题目内容
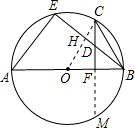
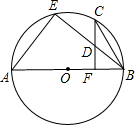 如图,AB为⊙O的直径,点C、E在半圆AB上,CF⊥AB于点F,BE交CF于点D,且∠BDF=2∠C
如图,AB为⊙O的直径,点C、E在半圆AB上,CF⊥AB于点F,BE交CF于点D,且∠BDF=2∠C
(1)求证: =
= ;
;
(2)若CF=8,OA=10,求BE的长.
(1)证明:延长CF交⊙O于M,
∵CF⊥AB,
∴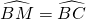 ,
,
∵∠BDF=2∠C,
∴∠C=∠DBC,
∴ ,
,
∴ ,
,
(2)解:连接OC,交BE于H,
∵ ,
,
∴OH⊥BE,
∵AB直径,
∴∠E=90°,
∴OH∥AE,
∴OH= AE,
AE,
∵在△OBH和△OCF中,
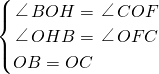 ,
,
∴△OBH≌△OCF(AAS),
∵OA=10,
∴OB=OC=10,
∴AB=20,
∴OH=OF=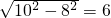 ,
,
∴AE=12,
∴BE=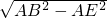 =
= =16.
=16.
分析:(1)延长CF交⊙O于M,由CF⊥AB,推出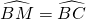 ,再由∠BDF=2∠C,推出∠C=∠DBC,求得
,再由∠BDF=2∠C,推出∠C=∠DBC,求得 后即可推出结论,
后即可推出结论,
(2)连接OC,交BE于H,根据(1)所推出的结论求得OH⊥BE,由AB直径,推出∠E=90°,求证OH∥AE,根据平行线的性质推出OH= AE后,通过求证△OBH和△OCF全等,结合勾股定理即可推出OH=OF=6,求出AE后,根据勾股定理即可求出BE=16.
AE后,通过求证△OBH和△OCF全等,结合勾股定理即可推出OH=OF=6,求出AE后,根据勾股定理即可求出BE=16.
点评:本题主要考查全等三角形的判定及性质,勾股定理的运用,垂径定理及圆周角定理等知识点,关键在于熟练应用相关的性质定理,(1)正确的做出辅助线,根据外角的性质,垂径定理,圆周角,弦的关系推出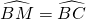 ,
, ,(2)连接OC后,根据相关的性质定理推出OH⊥BE,正确的推出OH=
,(2)连接OC后,根据相关的性质定理推出OH⊥BE,正确的推出OH= AE,关键在于求证△OBH≌△OCF.
AE,关键在于求证△OBH≌△OCF.
∵CF⊥AB,
∴
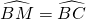 ,
,∵∠BDF=2∠C,
∴∠C=∠DBC,
∴
 ,
,∴
 ,
,(2)解:连接OC,交BE于H,
∵
 ,
,∴OH⊥BE,
∵AB直径,
∴∠E=90°,
∴OH∥AE,
∴OH=
 AE,
AE,∵在△OBH和△OCF中,
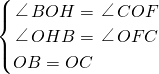 ,
,∴△OBH≌△OCF(AAS),
∵OA=10,
∴OB=OC=10,
∴AB=20,
∴OH=OF=
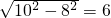 ,
,∴AE=12,
∴BE=
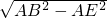 =
= =16.
=16.
分析:(1)延长CF交⊙O于M,由CF⊥AB,推出
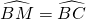 ,再由∠BDF=2∠C,推出∠C=∠DBC,求得
,再由∠BDF=2∠C,推出∠C=∠DBC,求得 后即可推出结论,
后即可推出结论,(2)连接OC,交BE于H,根据(1)所推出的结论求得OH⊥BE,由AB直径,推出∠E=90°,求证OH∥AE,根据平行线的性质推出OH=
 AE后,通过求证△OBH和△OCF全等,结合勾股定理即可推出OH=OF=6,求出AE后,根据勾股定理即可求出BE=16.
AE后,通过求证△OBH和△OCF全等,结合勾股定理即可推出OH=OF=6,求出AE后,根据勾股定理即可求出BE=16.点评:本题主要考查全等三角形的判定及性质,勾股定理的运用,垂径定理及圆周角定理等知识点,关键在于熟练应用相关的性质定理,(1)正确的做出辅助线,根据外角的性质,垂径定理,圆周角,弦的关系推出
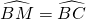 ,
, ,(2)连接OC后,根据相关的性质定理推出OH⊥BE,正确的推出OH=
,(2)连接OC后,根据相关的性质定理推出OH⊥BE,正确的推出OH= AE,关键在于求证△OBH≌△OCF.
AE,关键在于求证△OBH≌△OCF. 
练习册系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为