题目内容
关于x的一元二次方程x2-（2m-3）x+m2+1=0当m________时，方程有两个不相等的实数根；当m________时，此方程没有实数根；当m________时，此方程有两个相等的实数根．
＜
＞ =
分析：先计算△，要使方程有两个不相等的实数根，则△＞0；要使方程没有实数根，则△＜0；要使方程有两个相等的实数根，则△=0；分别解不等式或方程即可得到答案．
解答：∵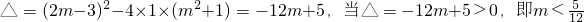
时，方程有两个不相等实根；
当△=-12m+5＜0，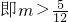
时，方程无实数根；
当△=-12m+5=0，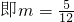
时，方程有两个相等的实数根．
故答案为m＜；m
；m=．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
＞ =分析：先计算△，要使方程有两个不相等的实数根，则△＞0；要使方程没有实数根，则△＜0；要使方程有两个相等的实数根，则△=0；分别解不等式或方程即可得到答案．
解答：∵
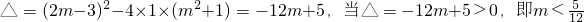时，方程有两个不相等实根；当△=-12m+5＜0，
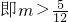时，方程无实数根；当△=-12m+5=0，
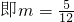时，方程有两个相等的实数根．故答案为m＜
；m；m=．点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
华东师大版一课一练系列答案
相关题目