题目内容
已知抛物线y=-x2+(m-2)x+3(m+1).
(1)求证:无论m为任何实数,抛物线与x轴总有交点;
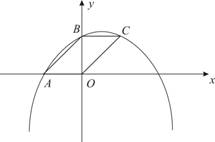
(2)设抛物线与y轴交于点C,当抛物线与x轴有两个交点A、B(点A在点B的左侧)时,如果∠CAB或∠CBA这两角中有一个角是钝角,那么m的取值范围是________;
(3)在(2)的条件下,P是抛物线的顶点,当△PAO的面积与△ABC的面积相等时求该抛物线的解析式.
答案:
解析:
解析:
|
(1) 证明:∵ ∴无论m为任何实数,抛物线与x轴总有交点. (2)m<-1且m≠-4. 3分(3) 解:令解得 x1=m+1,x2=-3. 4分 可求得顶点 ① 当A(m+1,0)、B(-3,0)时, ∵ ∴ 解得 ∴ ② 当A(-3,0)、B(m+1,0)时, 同理得 解得 ∴ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.
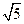 ,试求m的值;
,试求m的值; 直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函