题目内容
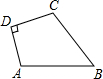 某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为
某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为36
36
m2.分析:连接AC,利用勾股定理列式求出AC,再利用勾股定理逆定理求出△ABC是直角三角形,然后根据这块田的面积=S△ADC+S△ABC列式计算即可得解.
解答: 解:如图,连接AC,根据勾股定理,AC=
解:如图,连接AC,根据勾股定理,AC=
=
=5m,
∵BC2+AC2=122+52=169=132=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴这块田的面积=S△ADC+S△ABC,
=
×3×4+
×5×12,
=6+30,
=36m2.
故答案为:36.
 解:如图,连接AC,根据勾股定理,AC=
解:如图,连接AC,根据勾股定理,AC=| AD2+AC2 |
| 32+42 |
∵BC2+AC2=122+52=169=132=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴这块田的面积=S△ADC+S△ABC,
=
| 1 |
| 2 |
| 1 |
| 2 |
=6+30,
=36m2.
故答案为:36.
点评:本题考查了勾股定理,勾股定理逆定理,作辅助线,把四边形分成两个直角三角形是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目

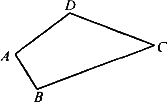

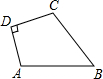 某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为________ m2.
某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为________ m2.