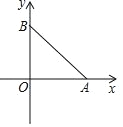Question

【题目】抛物线L：y=﹣x2+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B．

（1）直接写出抛物线L的解析式；

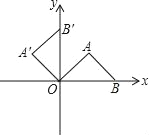
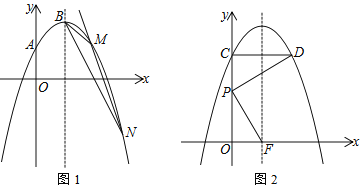
（2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N．若△BMN的面积等于1，求k的值；

（3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D．F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点．若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．

Answer 1

【答案】（1）y=﹣x2+2x+1；（2）-3；（3）当m=2﹣1时，点P的坐标为（0，）和（0，）；当m=2时，点P的坐标为（0，1）和（0，2）．

【解析】

（1）根据对称轴为直线x=1且抛物线过点A（0，1）利用待定系数法进行求解可即得；

（2）根据直线y=kx﹣k+4=k（x﹣1）+4知直线所过定点G坐标为（1，4），从而得出BG=2，由S△BMN=S△BNG﹣S△BMG=BGxN﹣BGxM=1得出xN﹣xM=1，联立直线和抛物线解析式求得x=，根据xN﹣xM=1列出关于k的方程，解之可得；

（3）设抛物线L1的解析式为y=﹣x2+2x+1+m，知C（0，1+m）、D（2，1+m）、F（1，0），再设P（0，t），分△PCD∽△POF和△PCD∽△POF两种情况，由对应边成比例得出关于t与m的方程，利用符合条件的点P恰有2个，结合方程的解的情况求解可得．

（1）由题意知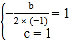，解得：，

∴抛物线L的解析式为y=﹣x2+2x+1；

（2）如图1，设M点的横坐标为xM，N点的横坐标为xN，

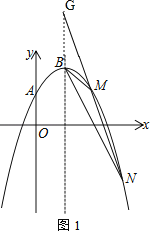
∵y=kx﹣k+4=k（x﹣1）+4，

∴当x=1时，y=4，即该直线所过定点G坐标为（1，4），

∵y=﹣x2+2x+1=﹣（x﹣1）2+2，

∴点B（1，2），

则BG=2，

∵S△BMN=1，即S△BNG﹣S△BMG=BG（xN﹣1）-BG（xM-1）=1，

∴xN﹣xM=1，

由得：x2+（k﹣2）x﹣k+3=0，

解得：x==，

则xN=、xM=，

由xN﹣xM=1得=1，

∴k=±3，

∵k＜0，

∴k=﹣3；

（3）如图2，

设抛物线L1的解析式为y=﹣x2+2x+1+m，

∴C（0，1+m）、D（2，1+m）、F（1，0），

设P（0，t），

（a）当△PCD∽△FOP时，，

∴，

∴t2﹣（1+m）t+2=0①；

(b)当△PCD∽△POF时，，

∴，

∴t=（m+1）②；

（Ⅰ）当方程①有两个相等实数根时，

△=（1+m）2﹣8=0，

解得：m=2﹣1（负值舍去），

此时方程①有两个相等实数根t1=t2=，

方程②有一个实数根t=，

∴m=2﹣1，

此时点P的坐标为（0，）和（0，）；

（Ⅱ）当方程①有两个不相等的实数根时，

把②代入①，得：（m+1）2﹣（m+1）+2=0，

解得：m=2（负值舍去），

此时，方程①有两个不相等的实数根t1=1、t2=2，

方程②有一个实数根t=1，

∴m=2，此时点P的坐标为（0，1）和（0，2）；

综上，当m=2﹣1时，点P的坐标为（0，）和（0，）；

当m=2时，点P的坐标为（0，1）和（0，2）．