题目内容
 如图,点P在x轴上,且
如图,点P在x轴上,且 ,点M也在x轴上,在OA上找点N,以P、M、N为顶点作正方形,则ON=________(如结果中有根号,请保留根号).
,点M也在x轴上,在OA上找点N,以P、M、N为顶点作正方形,则ON=________(如结果中有根号,请保留根号).
2或3- 或3+
或3+
分析:根据题意,因为PN是边还是对角线没有明确,所以分①PN是正方形的边长,②PN是正方形的对角线,且∠OPN=45°与∠OPN=135°两种情况进行讨论,设出ON的长度是2x,然后表示出正方形的边长与OP的长度,再根据OP的长度列式求解.
解答:设ON=2x,
①如图1,当PN是正方形的边长时,
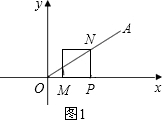
∵∠AOP=30°,
∴OP=2x•cos30°=2x× =
= x,
x,
又∵OP= ,
,
∴x=1,
∴ON=2x=2;
②如图2,PN是正方形的对角线,且∠OPN=45°时
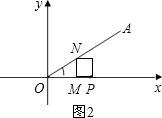
∵∠AOP=30°,
∴OM=2x•cos30°=2x× =
= x,
x,
MP=MN=ON•sin30°=2x× =x,
=x,
又∵OP= ,
,
∴ x+x=
x+x= ,
,
解得x=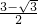 ,
,
∴ON=2x=3- ;
;
③如图3,PN是正方形的对角线,且∠OPN=135°时,
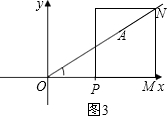
∵∠AOP=30°,
∴OM=2x•cos30°=2x× =
= x
x
MP=MN=ON•sin30°=2x× =x,
=x,
又∵OP= ,
,
∴ x-x=
x-x= ,
,
解得x=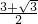 ,
,
∴ON=2x=3+ .
.
综上所述,ON的值为:2或3- 或3+
或3+ .
.
故答案为:2或3- 或3+
或3+ .
.
点评:本题主要考查了解直角三角形,坐标与图形的性质,利用了正方形的性质,30°角的正弦与余弦,难度不是很大,但要注意分情况讨论,容易漏解而导致出错.
 或3+
或3+
分析:根据题意,因为PN是边还是对角线没有明确,所以分①PN是正方形的边长,②PN是正方形的对角线,且∠OPN=45°与∠OPN=135°两种情况进行讨论,设出ON的长度是2x,然后表示出正方形的边长与OP的长度,再根据OP的长度列式求解.
解答:设ON=2x,
①如图1,当PN是正方形的边长时,

∵∠AOP=30°,
∴OP=2x•cos30°=2x×
 =
= x,
x,又∵OP=
 ,
,∴x=1,
∴ON=2x=2;
②如图2,PN是正方形的对角线,且∠OPN=45°时

∵∠AOP=30°,
∴OM=2x•cos30°=2x×
 =
= x,
x,MP=MN=ON•sin30°=2x×
 =x,
=x,又∵OP=
 ,
,∴
 x+x=
x+x= ,
,解得x=
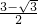 ,
,∴ON=2x=3-
 ;
;③如图3,PN是正方形的对角线,且∠OPN=135°时,

∵∠AOP=30°,
∴OM=2x•cos30°=2x×
 =
= x
xMP=MN=ON•sin30°=2x×
 =x,
=x,又∵OP=
 ,
,∴
 x-x=
x-x= ,
,解得x=
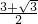 ,
,∴ON=2x=3+
 .
.综上所述,ON的值为:2或3-
 或3+
或3+ .
.故答案为:2或3-
 或3+
或3+ .
.点评:本题主要考查了解直角三角形,坐标与图形的性质,利用了正方形的性质,30°角的正弦与余弦,难度不是很大,但要注意分情况讨论,容易漏解而导致出错.

练习册系列答案
相关题目
 x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.
x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根. 如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为
如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为 -1)
-1) 交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.