题目内容
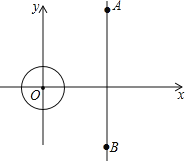
【题目】如图,在平面直角坐标系xOy中,![]() 的半径为1,A、B两点坐标分别为
的半径为1,A、B两点坐标分别为![]() 、
、![]() 已知点P是
已知点P是![]() 上的一点,点Q是线段AB上的一点,设
上的一点,点Q是线段AB上的一点,设![]() 的面积为S,当
的面积为S,当![]() 为直角三角形时,S的取值范围为______.
为直角三角形时,S的取值范围为______.
【答案】![]() ≤S≤
≤S≤![]() .
.
【解析】
根据△OPQ为直角三角形时,∠OQP不可能为90°,所以分两种情况:分别以O和P为直角顶点,根据直径所对的圆周角为直角,通过画辅助圆确定P和Q,画图,根据直角三角形面积公式计算可得结论.

解:①当P为直角顶点时,
当OQ最长时,如图1,OQ=5,Q与A重合,PQ=![]() =2
=2![]() ,S大=
,S大=![]() ×1×2
×1×2![]() =
=![]() ,
,
当OQ最短时,OQ=3,此时OQ⊥AB,PQ=![]() =2
=2![]() ,S小=
,S小=![]() =
=![]() ;
;
②当O为直角顶点时,如图2,
当Q与A重合时,OA最大,此时S=![]() ×1×5=
×1×5=![]() >
>![]() ,
,
当OQ⊥AB时,S最小,S=![]() =
=![]() ,
,
综上,当△OPQ为直角三角形时,S的取值范围为![]() ≤S≤
≤S≤![]() .
.
故答案为:![]() ≤ S ≤
≤ S ≤![]() .
.


练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目