题目内容
方程x(2x+1)=4(2x+1)的解为________.
x1= ,x2=4
,x2=4
分析:方程左右两边都含有因式(2x+1),可将其看作一个整体,然后再移项,分解因式求解.
解答:原方程可化为:x(2x+1)-4(2x+1)=0,
(2x+1)(x-4)=0,
解得:x1=- ,x2=4.
,x2=4.
点评:只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程.分解因式时,要根据情况灵活运用学过的因式分解的几种方法.
 ,x2=4
,x2=4分析:方程左右两边都含有因式(2x+1),可将其看作一个整体,然后再移项,分解因式求解.
解答:原方程可化为:x(2x+1)-4(2x+1)=0,
(2x+1)(x-4)=0,
解得:x1=-
 ,x2=4.
,x2=4.点评:只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程.分解因式时,要根据情况灵活运用学过的因式分解的几种方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
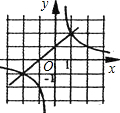 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y=