ΧβΡΩΡΎ»ί
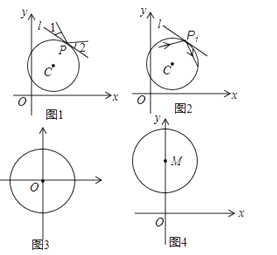
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§Ν§Ϋ”BDΘ§AD=6cmΘ§BD=8cmΘ§ΓœDBC=90ΓψΘ§œ÷ΫΪΓςAEF―ΊBDΒΡΖΫœρ‘»ΥΌΤΫ“ΤΘ§ΥΌΕ»ΈΣ2cm/sΘ§Ά§ ±Θ§ΒψG¥”ΒψD≥ωΖΔΘ§―ΊDCΒΡΖΫœρ‘»ΥΌ“ΤΕ·Θ§ΥΌΕ»ΈΣ2cm/sΘ°Β±ΓςAEFΆΘ÷Ι“ΤΕ· ±Θ§ΒψG“≤ΆΘ÷Ι‘ΥΕ·Θ§Ν§Ϋ”ADΘ§AGΘ§EGΘ§ΙΐΒψEΉςEHΓΆCD”ΎΒψHΘ§»γΆΦ2Υυ ΨΘ§…ηΓςAEFΒΡ“ΤΕ· ±ΦδΈΣtΘ®sΘ©Θ®0ΘΦtΘΦ4Θ©Θ°
Θ®1Θ©Β±t=1 ±Θ§«σEHΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©»τEGΓΆAGΘ§«σ÷ΛΘΚEG2=AEHGΘΜ
Θ®3Θ©…ηΓςAGDΒΡΟφΜΐΈΣyΘ®cm2Θ©Θ§Β±tΈΣΚΈ÷Β ±Θ§yΩ…»ΓΒΟΉν¥σ÷ΒΘ§≤Δ«σyΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΫβΘΚΘ®1Θ©ΓΏΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύADΓΈBCΘ§”÷ΓœDBC=90ΓψΘ§
ΓύΓœADB=90ΓψΘ§”÷AD=6cmΘ§BD=8cmΘ§
”…Ι¥Ι…Ε®άμΒΟΘ§AB=![]() =10cmΘ§
=10cmȧ
Β±t=1 ±Θ§EB=2cmΘ§
‘ρDE=8©¹2=6cmΘ§
ΓΏEHΓΆCDΘ§ΓœDBC=90ΓψΘ§
ΓύΓςDEHΓΉΓςDCBΘ§
Γύ![]() =
=![]() Θ§Φ¥
Θ§Φ¥![]() =
=![]() Θ§
Θ§
ΫβΒΟΘ§EH=3.6cmΘΜ
Θ®2Θ©ΓΏΓœCDB=ΓœAEFΘ§
ΓύAEΓΈCDΘ§
ΓύΓœAEG=ΓœEGHΘ§”÷EGΓΆAGΘ§EHΓΆCDΘ§
ΓύΓςAGEΓΉΓςEHGΘ§
Γύ![]() =
=![]() Θ§
Θ§
ΓύEG2=AEHGΘΜ
Θ®3Θ©”…Θ®1Θ©ΒΟΘ§ΓςDEHΓΉΓςDCBΘ§
Γύ![]() =
=![]() Θ§Φ¥
Θ§Φ¥![]() =
=![]() Θ§
Θ§
ΫβΒΟΘ§EH=![]() Θ§
Θ§
Γύy=![]() ΓΝDGΓΝEH=
ΓΝDGΓΝEH=![]() =©¹
=©¹![]() t2+
t2+![]() t=©¹
t=©¹![]() Θ®t©¹2Θ©2+
Θ®t©¹2Θ©2+![]() Θ§
Θ§
ΓύΒ±t=2 ±Θ§yΒΡΉν¥σ÷ΒΈΣ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΚΆΙ¥Ι…Ε®άμ«σ≥ωABΒΡ≥ΛΘ§÷ΛΟςΓςDEHΓΉΓςDCBΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫ±»άΐ ΫΘ§ΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©÷ΛΟςΓςAGEΓΉΓςEHGΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫ![]() =
=![]() Θ§ ’ϊάμΦ¥Ω…ΘΜ
Θ§ ’ϊάμΦ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΓςDEHΓΉΓςDCBΘ§«σ≥ωΚ· ΐΙΊœΒ ΫΘ§ΗυΨίΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΒΟΒΫ¥πΑΗΘ°
ΓΨΩΦΒψΨΪΈωΓΩ»œ’φ…σΧβΘ§ Ήœ»–η“ΣΝΥΫβΙ¥Ι…Ε®άμΒΡΗ≈Ρν(÷±Ϋ«»ΐΫ«–ΈΝΫ÷±Ϋ«±ΏaΓΔbΒΡΤΫΖΫΚΆΒ»”Ύ–±±ΏcΒΡΤΫΖΫ,Φ¥;a2+b2=c2)Θ§ΜΙ“Σ’ΤΈ’ΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ (ΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘±ΏœύΒ»«“ΤΫ––ΘΜΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œύΒ»Θ§ΝΎΫ«ΜΞ≤ΙΘΜΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œΏΜΞœύΤΫΖ÷)ΒΡœύΙΊ÷Σ Ε≤≈ «¥πΧβΒΡΙΊΦϋΘ°

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ