题目内容
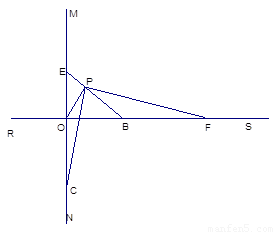
如图所示:直线MN⊥RS于点O,点B在射线OS上,OB=2,点C在射线ON上,OC=2,点E是射线OM上一动点,连结EB,过O作OP⊥EB于P,连结CP,过P作PF⊥PC交射线OS于F。
(1)求证:△POC∽△PBF。
(2)当OE=1,OE=2时, BF的长分别为多少?当OE=n时,BF=_______.
(3)当OE=1时,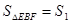 ;OE=2时,
;OE=2时,  ;…,OE=n时,
;…,OE=n时,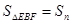 .则
.则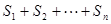 =_______.(直接写出答案)
=_______.(直接写出答案)
|
(1)证明:∵∠OPB=∠CPF
∴∠OPC=∠BPF ,
∵∠EOP=∠EOB=90,
∴∠EOP=∠OBP
∴∠POC=∠PBF
∴⊿POC∽⊿PBF
(2) 解∵ ⊿POC∽⊿PBF
∴OC/BF=PO/PB
∵⊿OPB∽⊿EOB
∴PO/PB=OE/OB
∴OC/BF= OE/OB
∴OE.BF=OC.OB=4
∴当OE=1时,BF=4;
当OE=2时,BF=2,当OE=n时,BF="4/n."
(3)根据题意得;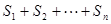 =2n;
=2n;
解析

练习册系列答案
相关题目
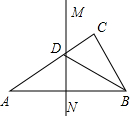
 12、如图所示,直线MN是线段AB的对称轴,点C在MN外,CA与MN相交于点D,如果CA+CB=4cm,那么△BCD的周长等于
12、如图所示,直线MN是线段AB的对称轴,点C在MN外,CA与MN相交于点D,如果CA+CB=4cm,那么△BCD的周长等于
 ;OE=2时,
;OE=2时,  ;…,OE=n时,
;…,OE=n时,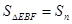 .则
.则 =_______.(直接写出答案)
=_______.(直接写出答案)