题目内容
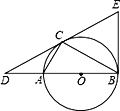
【题目】如图，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．
（1）当PC=CE时，求∠CDP的度数；
（2）试用等式表示线段PB、BC、CE之间的数量关系，并证明．
【答案】（1）22.5°；（2）
，证明见解析．
【解析】
（1）由
证明
，得出
，
，由等腰三角形的性质和三角形内角和定理得出
，即可得出结果；
（2）连接
，证明
，由勾股定理得出
，
，等量代换即可得．
解：（1）
四边形
是正方形，
，
，
，
，
在
和
中，
，
，
，，
，
，
，
，
；
（2），理由如下：
连接，如图所示：
由（1）得：，
，
∴
，
∵∠DCE=90°，
∴∠2+∠CEP=90°，
∵∠1=∠2，
∴∠1+∠CDP=90°，
∴∠DPE=90°，
∴
∵∠DCE=90°，
∴
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
