Question

若圆内接正三角形的边长为a，则边心距d=

3

6

a

．

Answer 1

分析：根据题意画出图形，连接OB，作OD⊥BC，由垂径定理可得到BD=

1

2

BC，再由等边三角形的性质可得到∠OBD的度数，由特殊角的三角函数值即可求解．

解答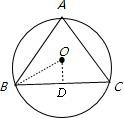：解：如图所示，连接OB，作OD⊥BC．
∵BC=a
∴BD=

1

2

BC=

a

2

，
∵△ABC是等边三角形，
∴∠OBD=30°，
∴OD=BD×tan30°=

a

2

×

3

3

=

3

6

a．
故答案为：

3

6

a．

点评：本题考查的是正多边形和圆及特殊角的三角函数值、垂径定理，根据题意画出图形利用数形结合求解是解答此题的关键．