题目内容
已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。 求该抛物线的解析式; 点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ。当△CQE的面积最大时,求点Q的坐标; 若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0)。
问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标若不存在,请说明理由。
(1)  (2) 当
(2) 当 时,
时, 有最大值3,此时
有最大值3,此时 .
.
(3) 所求点 的坐标为:
的坐标为: 或
或 或
或 或
或
解析试题分析:解:(1)由题意,得
解得
 所求抛物线的解析式为:
所求抛物线的解析式为: . (4分)
. (4分)
(2)设点 的坐标为
的坐标为 ,过点
,过点 作
作 轴于点
轴于点 .
.
由 ,得
,得 ,
, .
. 点
点 的坐标为
的坐标为 .
. ,
, .
. ,
, .
. ,
,
即 .
. .
.



 .
.
又 ,
, 当
当 时,
时, 有最大值3,此时
有最大值3,此时 .
.
(3)存在.
在 中.
中.
(ⅰ)若 ,
, ,
, .
.
又在 中,
中, ,
, .
. .
. .此时,点
.此时,点 的坐标为
的坐标为 .
.
由 ,得
,得 ,
, .
.
此时,点 的坐标为:
的坐标为: 或
或 . (10分)
. (10分)
(ⅱ)若 ,过点
,过点 作
作 轴于点
轴于点 ,
,
由等腰三角形的性质得: ,
, ,
, 在等腰直角
在等腰直角 中,
中, .
. .
.
由 ,得
,得 ,
, .
.
此时,点 的坐标为:
的坐标为: 或
或 . (12分)
. (12分)
(ⅲ)若 ,
, ,且
,且
 点
点 到
到 的距离为
的距离为 ,而
,而 ,
,
此时,不存在这样的直线 ,使得
,使得 是等腰三角形.(13分)
是等腰三角形.(13分)
综上所述,存在这样的直线 ,使得
,使得 是等腰三角形.所求点
是等腰三角形.所求点 的坐标为:
的坐标为:
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
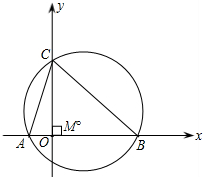 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.