题目内容
解方程组：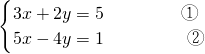
．
解：①×2，得：6x+4y=10…③
②+③，得：11x=11．
∴x=1．
把x=1代入①，得：3×1+2y=5
∴y=1．
所以此方程组的解是：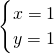
．
分析：利用加减消元法即可求得原方程组的解，将①×2+②，即可消去y的值，继而求得x的值，则可求得求得原方程组的解．
点评：此题考查了二元一次方程组的解法．此题难度不大，解题的关键是注意掌握方程组解法中的加减消元法和代入消元法，注意转化思想的应用．
②+③，得：11x=11．
∴x=1．
把x=1代入①，得：3×1+2y=5
∴y=1．
所以此方程组的解是：
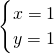．分析：利用加减消元法即可求得原方程组的解，将①×2+②，即可消去y的值，继而求得x的值，则可求得求得原方程组的解．
点评：此题考查了二元一次方程组的解法．此题难度不大，解题的关键是注意掌握方程组解法中的加减消元法和代入消元法，注意转化思想的应用．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
（1）解方程组：