题目内容
圆的内接正五边形和外接正六边形边长之比为________.
sin36°:
分析:根据题意画出图形,设圆的半径为1,进而利用锐角三角函数关系表示出AB,以及EF的长即可得出答案.
解答: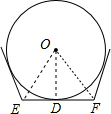
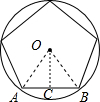 解:如图,设圆的半径为1,则OD=1,OA=OB=1,过点O作OC⊥AB,于点C,EF切圆于点D,
解:如图,设圆的半径为1,则OD=1,OA=OB=1,过点O作OC⊥AB,于点C,EF切圆于点D,
∵如图是圆的内接正五边形和外接正六边形,
∴∠AOB= =72°,∠EOF=
=72°,∠EOF= =60°,
=60°,
∴∠OBC=36°,
∵BC=OBsin36°=sin36°,
∴AB=2sin36°,
∵ =cos30°,
=cos30°,
∴FO=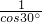 =
= ,
,
∴EF= ,
,
∴圆的内接正五边形和外接正六边形边长之比为:sin36°: ,
,
故答案为:sin36°: .
.
点评:此题主要考查了正多边形和圆的性质以及锐角三角函数关系等知识,正确表示出多边形的长是解题关键.

分析:根据题意画出图形,设圆的半径为1,进而利用锐角三角函数关系表示出AB,以及EF的长即可得出答案.
解答:

 解:如图,设圆的半径为1,则OD=1,OA=OB=1,过点O作OC⊥AB,于点C,EF切圆于点D,
解:如图,设圆的半径为1,则OD=1,OA=OB=1,过点O作OC⊥AB,于点C,EF切圆于点D,∵如图是圆的内接正五边形和外接正六边形,
∴∠AOB=
 =72°,∠EOF=
=72°,∠EOF= =60°,
=60°,∴∠OBC=36°,
∵BC=OBsin36°=sin36°,
∴AB=2sin36°,
∵
 =cos30°,
=cos30°,∴FO=
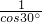 =
= ,
,∴EF=
 ,
,∴圆的内接正五边形和外接正六边形边长之比为:sin36°:
 ,
,故答案为:sin36°:
 .
.点评:此题主要考查了正多边形和圆的性质以及锐角三角函数关系等知识,正确表示出多边形的长是解题关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目