Question

【题目】某校九年级数学兴趣小组在探究相似多边形问题时，他们提出了下面两个观点：

观点一：将外面大三角形按图1的方式向内缩小，得到新三角形，它们对应的边间距都为，则新三角形与原三角形相似．

观点二：将邻边为和的矩形按图2方式向内缩小，得到新的矩形，它们对应的边间距都为，则新矩形与原矩形相似．

请回答下列问题：

（1）你认为上述两个观点是否正确？请说明理由．

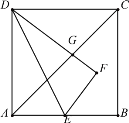
（2）如图3，已知，，，，将按图3的方式向外扩张，得到，它们对应的边间距都为，求的面积．

Answer 1

【答案】（1）观点一正确，观点二不正确，见解析；（2）54

【解析】

（1）根据相似三角形以及相似多边形的判定定理来判定甲乙的观点是否正确；
（2）首先根据勾股定理的逆定理求出∠C是直角，求出△ACB的内切圆半径，进而△DEF的内切圆的半径，根据相似三角形的性质以及面积公式即可求出△DEF的边长，进而求出△DEF的面积．

解：（1）答：观点一正确，观点二不正确．

理由：①如图1，连接并延长至，

和对应的边间距都为

，．

，．

．

即．同理．

观点一正确．

②如图2，由题意知，原矩形的邻边为和，则新矩形对应的邻边为和．

，，

，

新矩形与原矩形不相似．

观点二不正确．

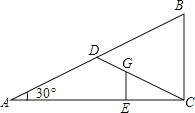
（2）如图3，作射线，交于点．

到边、的距离都为，

是的角平分线．

同理：是的角平分线，

点是与的内心．

，，，

是直角三角形．

设的内切圆半径为．则．解得：．

过作于点，交于点．

，

．

．

由（1）可知．

．同理．

，．

的面积为．