题目内容
小明投资销售一种进价为每件20元的护眼台灯.销售 过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.(3分)
(2)当销售单价定为多少元时,每月可获最大利润?每月最大利润是多少?(2分)
(3)如 果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)(3分)
果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)(3分)
解:(1)由题意,得:w = (x-20)·y=(x-20)·( )
) ,即w
,即w  (20≤x≤32)………………………….3
(20≤x≤32)………………………….3
(2)对于函数w  的图像的对称轴是直线
的图像的对称轴是直线 .
.
又∵a=-10<0,抛物线开口向下.
∴当20≤x≤32时,W随着X的增大而增大,
∴当X=32时,W=2160 …………………………5
答:当销售单价定为32元时,每月可获得最大利润,最大利润是2160元.
(3)取W=2000得,
解这个方程得:x1 = 30,x2 = 40.
∵a=-10<0,抛物线开口向下.
∴当30≤x≤40时,w≥2000.
∵20≤x≤32
∴当30≤x≤32时,w≥2000.
设每月的成本为P(元),由题意,得:


∵ ,
,
∴P随x的增大而减小.
∴当x = 32时,P的值最小,P最小值=3600.
答:想要每月获得的利润不低于2000元,小明每月的成本最少为3600元.
………………………………………8

练习册系列答案
相关题目


 ÷
÷ .
. 的图象上.若点A的坐标为(-2,-2),则k的值为
的图象上.若点A的坐标为(-2,-2),则k的值为 
 (B)
(B)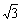 (C)
(C) (D)
(D)
 ,下列说法不正确的是( )
,下列说法不正确的是( ) (B) -2 (C)-3 (D)-18
(B) -2 (C)-3 (D)-18 
 )0+|﹣3|
)0+|﹣3|