题目内容
如图,已知:△ABC和△EDC中,AB=AC,EC=ED,∠BAC=∠CED.点A、D在直线C的同侧.

(1)当B、C、E在同一直线上时,且∠BAC=60°(如图1).则∠AFB=
(2)将图1中的△ABC绕点C旋转(点F不与点A、B重合),得到图2或图3.
①若∠BAC=α,则在图2中,求∠AFB(用含α的式子表示);
②在图3中,图2中的结论是否还成立?若成立,说明理由;若不成立,它等于什么?并写出推理过程.

(1)当B、C、E在同一直线上时,且∠BAC=60°(如图1).则∠AFB=
60
60
°;(2)将图1中的△ABC绕点C旋转(点F不与点A、B重合),得到图2或图3.
①若∠BAC=α,则在图2中,求∠AFB(用含α的式子表示);
②在图3中,图2中的结论是否还成立?若成立,说明理由;若不成立,它等于什么?并写出推理过程.
分析:(1)由题意易得△ABC∽△EDC,进一步证得△BCD∽△ACE,进而可得∠AFB=∠CBD+∠AEC=∠CAE+∠AEC=∠ACB=60°;
(2)①由前面步骤可得∠AFB=180°-∠CAE-∠BAC-∠ABD=180°-∠BAC-∠ABC=∠ACB=90°-
α;
②与前面步骤相同,可求得∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED,代入数据求大小.
(2)①由前面步骤可得∠AFB=180°-∠CAE-∠BAC-∠ABD=180°-∠BAC-∠ABC=∠ACB=90°-
| 1 |
| 2 |
②与前面步骤相同,可求得∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED,代入数据求大小.
解答:解:(1)∠AFB=60°,
∵AB=AC,EC=ED,∠BAC=∠CED=60°,
∴△ABC∽△EDC,
∴∠CBD=∠CAE,
∴∠AFB=180°-∠CAE-∠BAC-∠ABD,
=180°-∠BAC-∠ABC,
=∠ACB,
∴∠AFB=60°;
故答案为60°;
(2)①∵AB=AC,EC=ED,∠BAC=∠CED,
∴△ABC∽△EDC,
∴∠ACB=∠ECD,
=
,
∴△BCD∽△ACE,
∴∠CBD=∠CAE,
∴∠AFB=180°-∠CAE-∠BAC-∠ABD,
=180°-∠BAC-∠ABC=∠ACB,
∵AB=AC,∠BAC=α,
∴∠ACB=90°-
α,
∴∠AFB=90°-
α,
②图2中的结论不成立?若成立,它等于90°+
α,
理由如下:
∵AB=AC,EC=ED,∠BAC=∠CED,
∴△ABC∽△EDC,
∴∠ACB=∠ECD,
=
,
∴△BCD∽△ACE,
∴∠CBD=∠CAE,
∴∠BDC=∠AEC,
∴∠AFB=∠BDC+∠CDE+∠DEF,
=∠CDE+∠CED=180°-∠DCE,
∵AB=AC,EC=ED,∠BAC=∠DEC=α,
∴∠DCE=90°-
α,
∴∠AFB=180°-(90°-
α)=90°+
α.
∵AB=AC,EC=ED,∠BAC=∠CED=60°,
∴△ABC∽△EDC,
∴∠CBD=∠CAE,
∴∠AFB=180°-∠CAE-∠BAC-∠ABD,
=180°-∠BAC-∠ABC,
=∠ACB,

∴∠AFB=60°;
故答案为60°;
(2)①∵AB=AC,EC=ED,∠BAC=∠CED,
∴△ABC∽△EDC,
∴∠ACB=∠ECD,
| BC |
| DC |
| AC |
| CE |
∴△BCD∽△ACE,
∴∠CBD=∠CAE,
∴∠AFB=180°-∠CAE-∠BAC-∠ABD,
=180°-∠BAC-∠ABC=∠ACB,
∵AB=AC,∠BAC=α,
∴∠ACB=90°-
| 1 |
| 2 |
∴∠AFB=90°-
| 1 |
| 2 |
②图2中的结论不成立?若成立,它等于90°+
| 1 |
| 2 |
理由如下:
∵AB=AC,EC=ED,∠BAC=∠CED,
∴△ABC∽△EDC,
∴∠ACB=∠ECD,
| BC |
| DC |
| AC |
| CE |
∴△BCD∽△ACE,
∴∠CBD=∠CAE,
∴∠BDC=∠AEC,
∴∠AFB=∠BDC+∠CDE+∠DEF,
=∠CDE+∠CED=180°-∠DCE,
∵AB=AC,EC=ED,∠BAC=∠DEC=α,
∴∠DCE=90°-
| 1 |
| 2 |
∴∠AFB=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了相似三角形的判定与性质及等边三角形的性质;解题时应根据图形旋转的变化规律,探究两个角之间的数量关系.并且本题突出考查从特殊与一般的数学思想和实验研究的能力,让学生经历了动手操作、观察猜想、合情推理、归纳证明等全过程,题目的难度不小.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
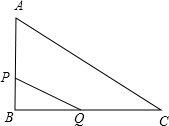
 如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF. 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE. 如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则
如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则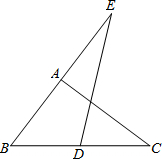 如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,
如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,