题目内容
如图，已知直线l1∥l2∥l3∥l4∥l5，相邻两条平行直线间的距离都相等，如果直角梯形ABCD的三个顶点在平行直线上，∠ABC=90°且AB=3AD，则tanα=分析：利用三角形相似的判定求出假设AE=4y，DF=
y，AF=y，即可得出∠α的值．
| 4 |
| 3 |
解答：
解：做AE⊥l5，垂足为E，
∵直线l1∥l2∥l3∥l4∥l5，相邻两条平行直线间的距离都相等，直角梯形ABCD的三个顶点在平行直线上，∠ABC=90°，
∴∠BAE+∠EAD=90°，∠α+∠DAF=90°，
∴∠α=∠BAE，∠AEB=∠AFD，
∴△ABE∽△DAF，
∵且AB=3AD，AB÷AD=3，
假设AE=4y，
∴DF=
y，AF=y，
∴tanα=
=
，
故答案为：
．
解：做AE⊥l5，垂足为E，∵直线l1∥l2∥l3∥l4∥l5，相邻两条平行直线间的距离都相等，直角梯形ABCD的三个顶点在平行直线上，∠ABC=90°，
∴∠BAE+∠EAD=90°，∠α+∠DAF=90°，
∴∠α=∠BAE，∠AEB=∠AFD，
∴△ABE∽△DAF，
∵且AB=3AD，AB÷AD=3，
假设AE=4y，
∴DF=
| 4 |
| 3 |
∴tanα=
| AF |
| DF |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：此题主要考查了锐角三角函数的定义以及直角梯形的性质以及平行线分线段成比例定理，作出垂足利用相似三角形性质求出AF与DF是解决问题的关键．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
6、如图，已知直线l1，l2，l3相交于点O，∠1=35°，∠2=25°，则∠3等于（ ）
（2012•郯城县一模）如图，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，则cosα=（ ）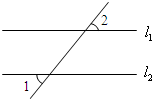
（2007•黔南州）如图，已知直线l1∥l2，∠1=50°，那么∠2=
如图：已知直线l1∥l2，且l3、l4和l1、l2分别交于点A、B和点C、D，点P在AB上，设∠ADP=∠1，∠DPC=∠2，∠BCP=∠3．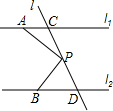
如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P与点C、D不重合），点A在直线l1上，点B在直线l2上．