题目内容
解方程: .
.
解:将原方程变形为 +
+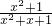 =
= +
+ .
.
设y= ,则原方程变为y+
,则原方程变为y+ =
= +
+ ,
,
解得y1= ,y2=
,y2= .
.
当 =
= 时,x=
时,x= ;
;
当 =
= 时,x=1.
时,x=1.
经检验,x= 及x=1均是原方程的根.
及x=1均是原方程的根.
故原方程的根是x= 及x=1.
及x=1.
分析:观察方程,发现等号左边第一个分式的分子与第二个分式的分母相同,又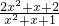 =1+
=1+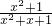 ,故可设y=
,故可设y= ,运用换元法解此方程,结果需要检验.
,运用换元法解此方程,结果需要检验.
点评:本题考查了分式方程的解法.解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.注意解分式方程一定要验根.本题通过观察,能够将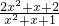 变形为1+
变形为1+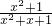 ,是解题的关键.
,是解题的关键.
 +
+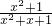 =
= +
+ .
.设y=
 ,则原方程变为y+
,则原方程变为y+ =
= +
+ ,
,解得y1=
 ,y2=
,y2= .
.当
 =
= 时,x=
时,x= ;
;当
 =
= 时,x=1.
时,x=1.经检验,x=
 及x=1均是原方程的根.
及x=1均是原方程的根.故原方程的根是x=
 及x=1.
及x=1.分析:观察方程,发现等号左边第一个分式的分子与第二个分式的分母相同,又
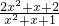 =1+
=1+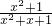 ,故可设y=
,故可设y= ,运用换元法解此方程,结果需要检验.
,运用换元法解此方程,结果需要检验.点评:本题考查了分式方程的解法.解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.注意解分式方程一定要验根.本题通过观察,能够将
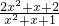 变形为1+
变形为1+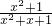 ,是解题的关键.
,是解题的关键. 
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目