Question

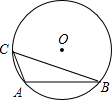如图，⊙O 是△ABC 的外接圆，BC=a，CA=b，且∠A-∠B=90°．则⊙O的半径为________．

Answer 1

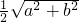
分析：首先作直径BD，连接AD，CD，由半圆（或直径）所对的圆周角是直角，即可得∠DAB=∠DCB=90°，又由∠A-∠B=90°，求得∠CAD=∠CBA，继而求得CD=CA=b，然后由勾股定理即可求得直径BD的长，则可求得⊙O的半径．
解答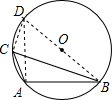：解：作直径BD，连接AD，CD，
则∠DAB=∠DCB=90°，
∵∠CAB-∠ABC=90°，∠CAB-∠CAD=90°，
∴∠CAD=∠ABC，
∴=，
∴CD=AC=b，
∵BC=a，
∴BD==，
∴⊙O的半径为：．
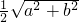故答案为：．
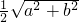点评：此题考查了圆周角定理与勾股定理．此题难度适中，解题的关键是准确作出辅助线，掌握数形结合思想的应用．