题目内容
 如图,AD⊥BC于D,若AD=BD,BE=AC,∠A=28°,则∠BED=
如图,AD⊥BC于D,若AD=BD,BE=AC,∠A=28°,则∠BED=62
62
度.分析:根据HL证Rt△BDE≌Rt△ADC,根据全等三角形的性质可得∠BED=∠C,再根据直角三角形两锐角互余可得答案.
解答:证明:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
,
∴Rt△BDE≌Rt△ADC(HL),
∴∠BED=∠C,
∵∠A=28°,
∴∠C=90°-28°=62°,
∴∠BED=62°,
故答案为:62.
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
|
∴Rt△BDE≌Rt△ADC(HL),
∴∠BED=∠C,
∵∠A=28°,
∴∠C=90°-28°=62°,
∴∠BED=62°,
故答案为:62.
点评:本题主要考查三角形全等的判定方法和性质,关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 15、如图,AD⊥BC于D,DE∥AC,则∠C与∠ADE之和为
15、如图,AD⊥BC于D,DE∥AC,则∠C与∠ADE之和为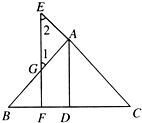 23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2. 22、如图,AD⊥BC于D,EF⊥BC于F,且∠E=∠1,求证∠BAD=∠CAD.
22、如图,AD⊥BC于D,EF⊥BC于F,且∠E=∠1,求证∠BAD=∠CAD. 23、如图,AD⊥BC于D,EF⊥BC于E,∠1=∠2,AB与DG平行吗?为什么?
23、如图,AD⊥BC于D,EF⊥BC于E,∠1=∠2,AB与DG平行吗?为什么? (2013•义乌市)如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC=
(2013•义乌市)如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC=