题目内容
某产品每件成本30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
| x(元) | 40 | 50 | 60 | … |
| y(件) | 60 | 50 | 40 | … |
(1)求出这个一次函数关系式;
(2)设每日的销售利润为w(元),售价为x(元),求出w与x的函数关系式.
(3)每件产品的销售价应定为多少元时销售利润最大?此时销售利润是多少元?
解:(1)将(40,60)和(50,50)代入y=kx+b,
得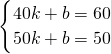 ,
,
解得,k=-1,b=100,
所求一次函数解析式为y=-x+100;
(2)每件产品的销售价应定为x元,所获销售利润为w元,
w=(x-30)(100-x),
=-x2+130x-3000;
(3)将二次函数w=-x2+130x-3000配方,得
W=-(x-65)2+1225,
∵a=-1<0,
∴当x=65时,W取得最大值1225,
∴产品的销售价应定为65元,此时每日获得最大销售利润为1225元.
分析:(1)设一次函数y=kx+b,利用“两点法”求一次函数解析式;
(2)根据利润w=(售价-进价)×销售量y,列出函数关系式;
(3)将(2)的函数关系式配方,得出顶点式,求函数的最大值.
点评:本题考查了二次函数的运用.关键是根据题意,列出相应的函数关系式,运用二次函数的性质解题.
得
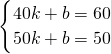 ,
,解得,k=-1,b=100,
所求一次函数解析式为y=-x+100;
(2)每件产品的销售价应定为x元,所获销售利润为w元,
w=(x-30)(100-x),
=-x2+130x-3000;
(3)将二次函数w=-x2+130x-3000配方,得
W=-(x-65)2+1225,
∵a=-1<0,
∴当x=65时,W取得最大值1225,
∴产品的销售价应定为65元,此时每日获得最大销售利润为1225元.
分析:(1)设一次函数y=kx+b,利用“两点法”求一次函数解析式;
(2)根据利润w=(售价-进价)×销售量y,列出函数关系式;
(3)将(2)的函数关系式配方,得出顶点式,求函数的最大值.
点评:本题考查了二次函数的运用.关键是根据题意,列出相应的函数关系式,运用二次函数的性质解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某产品每件成本10元,试销阶段每件产品的日销售价x(元)与产品的日销售量y(件)之间的关系如下表:
(1)请在直角坐标系上描点,观察点的分布,建立y与x的恰当函数模型.
(2)若要求每天卖出24件,则这一天它能获利多少元?
| x(元) | 15 | 20 | 25 | 30 | … |
| y(件) | 25 | 20 | 15 | 10 | … |
(2)若要求每天卖出24件,则这一天它能获利多少元?
某产品每件成本30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y(件)与销售价x(元)满足一次函数y=kx+b.
(1)求出这个一次函数关系式;
(2)设每日的销售利润为w(元),售价为x(元),求出w与x的函数关系式.
(3)每件产品的销售价应定为多少元时销售利润最大?此时销售利润是多少元?
| x(元) | 40 | 50 | 60 | … |
| y(件) | 60 | 50 | 40 | … |
(1)求出这个一次函数关系式;
(2)设每日的销售利润为w(元),售价为x(元),求出w与x的函数关系式.
(3)每件产品的销售价应定为多少元时销售利润最大?此时销售利润是多少元?
某产品每件成本30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y(件)与销售价x(元)满足一次函数y=kx+b.
(1)求出这个一次函数关系式;
(2)设每日的销售利润为w(元),售价为x(元),求出w与x的函数关系式.
(3)每件产品的销售价应定为多少元时销售利润最大?此时销售利润是多少元?
| x(元) | 40 | 50 | 60 | … |
| y(件) | 60 | 50 | 40 | … |
(1)求出这个一次函数关系式;
(2)设每日的销售利润为w(元),售价为x(元),求出w与x的函数关系式.
(3)每件产品的销售价应定为多少元时销售利润最大?此时销售利润是多少元?