题目内容
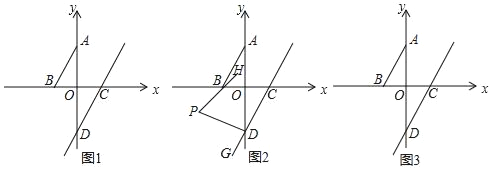
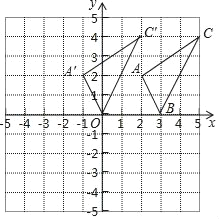
【题目】如图，在平面直角坐标系中，将三角形ABC向左平移至点B与原点重合，得三角形A′OC′．
（1）直接写出三角形ABC的三个顶点的坐标A B C ；
（2）画出三角形A′OC′；
（3）求三角形ABC的面积；
（4）直接与出A′C′与y轴交点的坐标 ．
【答案】（1）（2，2），（3，0），（5，4）；（2）见解析；（3）4；（4）（0，
）
【解析】
（1）利用第一象限点的坐标特征写出A、B、C三点的坐标；
（2）利用点平移的规律写出平移后A′、C′点的坐标，然后顺次连接点A′、O、C′即可；
（3）用一个矩形的面积分别减去三个直角三角形的面积可计算出△ABC的面积；
（4）先利用待定系数法求出直线A′C′的解析式，然后计算自变量为0所对应的自变量的值，从而得到直线A′C′与y轴交点的坐标．
解：（1）A、B、C点的坐标为（2，2），（3，0），（5，4）；
（2）如图，三角形A′OC′为所作；
（3）三角形ABC的面积＝3×4﹣
×2×1﹣×2×3﹣×2×4＝4；
（4）A′（﹣1，2），C′（2，4），
设直线A′C′的解析式为y＝kx+b，
把A′（﹣1，2），C′（2，4）代入得
，解得
，
∴直线A′C′的解析式为y＝
x+ ，
当x＝0时，y＝ x+ ＝ ，
∴直线A′C′与y轴的交点坐标为（0， ）．
故答案为：（1）（2，2），（3，0），（5，4）；（2）见解析；（3）4；（4）（0，）.
【题目】红星中学计划组织“春季研修活动，活动组织负责人从公交公司了解到如下租车信息：
车型 |
|
|
载客量（人/辆） |
|
|
租金（元/辆） |
|
|
校方从实际情况出发,决定租用
、
型客车共
辆，而且租车费用不超过
元。
（1）请为校方设计可能的租车方案；
（2）在（1）的条件下，校方根据自愿的原则，统计发现有
人参加，请问校方应如何租车，且又省钱?
