题目内容
已知抛物线y1=a1x2+b1x+c1,y2=a2x2+b2x+c2,且满足
=
=
=k(k≠0,1),则称抛物线y1,y2互为“友好抛物线”,则下列关于“友好抛物线”的说法:
①y1,y2开口方向,开口大小不一定相同;
②y1,y2的对称轴相同;
③如果y2的最值为m,则y1的最值为km;
④如果y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离为|k|d.
正确的是
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
①y1,y2开口方向,开口大小不一定相同;
②y1,y2的对称轴相同;
③如果y2的最值为m,则y1的最值为km;
④如果y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离为|k|d.
正确的是
①②③
①②③
(请填序号)分析:根据友好抛物线的条件,a1、a2的符号不一定相同,即可得到开口方向、开口大小不一定相同,代入对称轴-
和
即可判断②、③,根据根与系数的关系求出与X轴的两交点的距离|g-e|和|d-m|,即可判断④.
| b |
| 2a |
| 4ac-b2 |
| 4a |
解答:解:由已知可知:a1=ka2,b1=kb2,c1=kc2,
①根据友好抛物线的条件,a1、a2的符号不一定相同,所以开口方向、开口大小不一定相同,故本选项正确;
②因为
=
=k,代入-
得到对称轴相同,故本选项正确;
③因为如果y2的最值是m,则y1的最值是
=k•
=km,故本选项正确;
④因为设直线y1于x轴的交点坐标是(e,f),(g,h),则e+g=-
,eg=
,
直线y2于x轴的交点坐标是(m,n),(d,p),则m+d=-
,md=
,
可求得:|g-e|=|d-m|=
,故本选项错误.
故答案为:①②③.
①根据友好抛物线的条件,a1、a2的符号不一定相同,所以开口方向、开口大小不一定相同,故本选项正确;
②因为
| a1 |
| a2 |
| b1 |
| b2 |
| b |
| 2a |
③因为如果y2的最值是m,则y1的最值是
| 4a1c1-b2 |
| 4a1 |
| 4a2c2-b2 |
| 4a2 |
④因为设直线y1于x轴的交点坐标是(e,f),(g,h),则e+g=-
| b1 |
| a1 |
| c1 |
| a1 |
直线y2于x轴的交点坐标是(m,n),(d,p),则m+d=-
| b2 |
| a2 |
| c2 |
| a2 |
可求得:|g-e|=|d-m|=
|
故答案为:①②③.
点评:本题主要考查了二次函数图象上点的坐标特征,抛物线于X轴的交点,二次函数的最值等知识点解此题的关键是能根据友好抛物线的条件进行判断.

练习册系列答案
相关题目

 (2013•南昌)已知抛物线yn=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(2013•南昌)已知抛物线yn=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.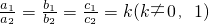 ,则我们称抛物线y1与y2互为“友好抛物线”,请写出当
,则我们称抛物线y1与y2互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标. ,则我们称抛物线y1与y2互为“友好抛物线”,请写出当
,则我们称抛物线y1与y2互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.