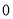题目内容
(本题满分11分)如图,△ 中,
中, ,以边
,以边 为直径作
为直径作 ,交
,交 于点
于点 ,过
,过 作
作 于点
于点 .
.

(1)求证: 为
为 的切线;
的切线;
(2)若 ,
, ,求
,求 的长.
的长.
(1)见解析;(2) .
.
【解析】
试题分析:(1)连接 与
与 ,只需证明
,只需证明 ⊥
⊥ 即可,根据三线合一可得
即可,根据三线合一可得 为
为 的中点,然后根据三角形的中位线定理可证
的中点,然后根据三角形的中位线定理可证 ∥
∥ ,因为
,因为 ,所以
,所以 ⊥
⊥ ;(2)先根据
;(2)先根据 ,
, ,求出线段
,求出线段 ,然后根据勾股定理可得BD=CD=5,然后利用△
,然后根据勾股定理可得BD=CD=5,然后利用△ ∽△
∽△ ,可求出
,可求出 的长;也可先利用sinC=
的长;也可先利用sinC= 求出DE的长,在利用勾股定理求出
求出DE的长,在利用勾股定理求出 的长.
的长.
试题解析:(1)证明:连接 与
与

∵ 是
是 的直径,∴
的直径,∴
即
∵ ,∴
,∴ 且
且
即 为
为 的中点
的中点
∵ 为
为 的中点,∴
的中点,∴ ∥
∥
∵ ,∴
,∴ ⊥
⊥
∴ 为
为 的切线.
的切线.
(2)【解析】
∵ ,
, ,
,
∴ ,即
,即
∴ ,∴
,∴ .
.
在△ 和△
和△ 中,
中, ,
,
∴△ ∽△
∽△ ,
, .
.
∴ .
.
考点:1.等腰三角形的性质;2.勾股定理;3.三角函数;4.相似三角形的判定与性质.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 .
.

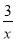 ,②
,②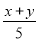 ,③
,③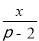 ,④
,④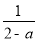 中,是分式的有
中,是分式的有 点测得
点测得 ,在
,在 点测得
点测得 ,且
,且 米,则这段河岸的宽度为_____________.
米,则这段河岸的宽度为_____________.
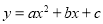 的对称轴为
的对称轴为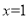 ,与
,与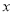 轴的一个交点
轴的一个交点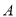 在(2,0)和(3,0)之间,其
在(2,0)和(3,0)之间,其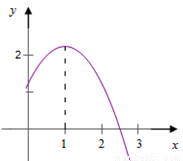
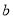 <
<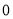 B.
B.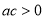 C.
C.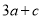
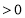 D.
D.