题目内容
 如图,已知圆锥的母线长OA=6,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处.则小虫所走的最短距离为
如图,已知圆锥的母线长OA=6,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处.则小虫所走的最短距离为
- A.12
- B.4π
- C.
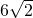
- D.

D
分析:利用圆锥的底面周长等于侧面展开图的弧长可得圆锥侧面展开图的圆心角,求出侧面展开图中两点间的距离即为最短距离.
解答: 解:∵底面圆的半径为2,
解:∵底面圆的半径为2,
∴圆锥的底面周长为2π×2=4π,
设圆锥的侧面展开图的圆心角为n.
∴ =4π,
=4π,
解得n=120°,
作OC⊥AA′于点C,
∴∠AOC=60°,
∴AC=OA×sin60°=3 ,
,
∴AA′=2AC=6 .
.
故选D.
点评:考查圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.
分析:利用圆锥的底面周长等于侧面展开图的弧长可得圆锥侧面展开图的圆心角,求出侧面展开图中两点间的距离即为最短距离.
解答:
 解:∵底面圆的半径为2,
解:∵底面圆的半径为2,∴圆锥的底面周长为2π×2=4π,
设圆锥的侧面展开图的圆心角为n.
∴
 =4π,
=4π,解得n=120°,
作OC⊥AA′于点C,
∴∠AOC=60°,
∴AC=OA×sin60°=3
 ,
,∴AA′=2AC=6
 .
.故选D.
点评:考查圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,已知圆锥的母线长OA=6,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处.则小虫所走的最短距离为( )
如图,已知圆锥的母线长OA=6,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处.则小虫所走的最短距离为( )| A、12 | ||
| B、4π | ||
C、6
| ||
D、6
|
 如图,已知圆锥的母线长OA=8,底面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到了A点,求小虫爬行的最短路线的长.
如图,已知圆锥的母线长OA=8,底面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到了A点,求小虫爬行的最短路线的长.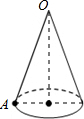 (2012•南海区三模)如图,已知圆锥的母线OA=8,底面圆的半径r=2,若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是
(2012•南海区三模)如图,已知圆锥的母线OA=8,底面圆的半径r=2,若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是 如图,已知圆锥的母线为10,底面圆的直径为12,则此圆锥的侧面积是( )
如图,已知圆锥的母线为10,底面圆的直径为12,则此圆锥的侧面积是( ) 如图,已知圆锥的母线AC=6cm,侧面展开图是半圆,则底面半径OC=
如图,已知圆锥的母线AC=6cm,侧面展开图是半圆,则底面半径OC=