Question

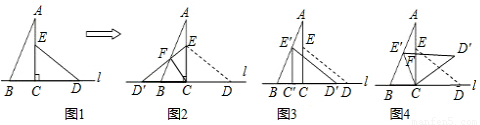
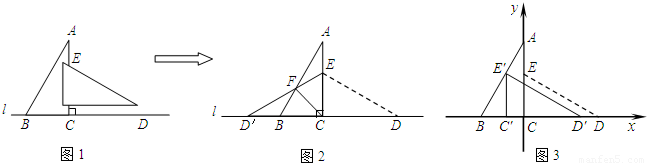
将两块形状大小完全相同的直角三角板按如图1所示的方式拼在一起．它们中较小直角边的长为6cm，较小锐角的度数为30°．
（1）将△ECD沿直线AC翻折到如图2的位置，连接CF，图中除了△ABC≌△ECD≌△ECD′外，还有没有全等的三角形？若有，请指出一对并给出证明．
（2）以点C为坐标原点建立如图3所示的直角坐标系，将△ECD沿x轴向左平移，使E点落在AB上，请求出点E′的坐标．

Answer 1

【答案】分析：（1）利用全等三角形的性质可以证明∠A=∠D′，AC=D′C，BC=EC，从而证得AE=D′B，利用AAS证明△AEF≌△D′BF；
（2）在Rt△B′BC′中，利用三角函数即可求得BC′的长，则CC′的长度可以求得，C′的坐标即可得到．
解答：解：（1）△AEF≌△D′BF，（△ACF与△D′CF，△ECF与△BCF．）
证明：∵△ABC≌△D′EC，
∴∠A=∠D′，AC=D′C，BC=EC，
∴AE=D′B
在∴△AEF和△D′BF中，

∴△AEF≌△D′BF
（2）在Rt△B′BC′中，BC′=2，所以CC′=6-2，所以E′（2-6，6）．
点评：本题考查了全等三角形的判定与性质，求点的坐标的问题一般的思路就是转化为求线段的长度的问题．