Question

【题目】如图，二次函数的图像与轴交于点，与轴交于点，顶点的横坐标为.

（1）求二次函数的表达式及的坐标；

（2）若 ()是轴上一点， ，将点绕着点顺时针方向旋转得到点.当点恰好在该二次函数的图像上时，求的值；

（3）在（2）的条件下，连接.若是该二次函数图像上一点，且，求点的坐标.

Answer 1

【答案】（1）二次函数的表达式为， ， ；

（2）t的值为-2；

（3）或

【解析】试题分析：（1）由D点的横坐标可求出m的值，从而确定二次函数表达式，令y=0，可求出x的值，从而确定A，B点的坐标；

（2）由旋转得E(-t,5+t)，代入二次函数表达式，从而求出t的值；

（3）分点在轴上方和点在轴下方两种情况进行讨论，设点，过点作轴于点，过点作轴于点.利用△∽△即可求解.

试题解析：（1）由题意，得，解得， （舍去）

∴二次函数的表达式为

当时， ，解得， ，∴，

（2）如图，过点作轴于点，

易证△≌△，

∴，

∴

当点恰好在该二次函数的图像上时，有

解得， （舍去）

（3）设点

①若点在轴上方，

如图，过点作轴于点，

过点作轴于点.

∵，

∴

∴△∽△

∴， 即

∴， （舍去）

∴

②若点在轴下方，

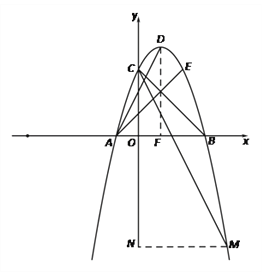
如图，过点作轴于点，

过点作轴于点.

∵，

∴

∴△∽△

∴， 即

∴， （舍去）

∴

综上所述， 或