��Ŀ����
��������y=ax2+bx+c��a��0����x���ڵ�A��x1��0��B��x2��0����x1��0��x2��0����y�� �ڵ�C������ΪP���������ߵĶԳ���Ϊֱ��x=1����S��AOC��S��BOC=1��3��
�ڵ�C������ΪP���������ߵĶԳ���Ϊֱ��x=1����S��AOC��S��BOC=1��3����1����������ߵĽ���ʽ���ú�a��ʽ�ӱ�ʾ����
��2�����A��B��C�����Բ��Բ��ΪM��MO���ӳ��߽���M�ڵ�F����ֱ��PC�Ľ���ʽΪy=-x-3ʱ����AC��뾶AM��CM��Χ�����ε����������F�����M���е�ֱ��L�Ľ���ʽ��
��3���ڣ�1�����£���ABC�ܷ��Ϊ�۽������Σ��ܷ��Ϊ���������Σ����ܣ������Ӧ��aֵ��aֵ�ķ�Χ�������ܣ���˵�����ɣ�
��������1������S��AOC��S��BOC=1��3���ɵõ�OA��OB��ֵ���ٸ��ݶԳ��ᣬ�������OA��OB�ij����õ�A��B�����꣬�Ӷ���ú�������ʽ��
��2��C��ֱ��y=-x-3�ϣ��������C�����꣬�������ε������ʽ����������ε������Ȼ����������ε������Լ����ഹֱ����ֱ�ߵĹ�ϵ������ߵĽ���ʽ��
��3�����ɶ۽������������ߵ�ƽ���ʹ��ڵ����ߵ�ƽ�����ݴ˼��ɵõ�����a�IJ���ʽ�����a��ֵ�����ǵ��������Σ���������ۣ��ⷽ�̼������a��ֵ��
��2��C��ֱ��y=-x-3�ϣ��������C�����꣬�������ε������ʽ����������ε������Ȼ����������ε������Լ����ഹֱ����ֱ�ߵĹ�ϵ������ߵĽ���ʽ��
��3�����ɶ۽������������ߵ�ƽ���ʹ��ڵ����ߵ�ƽ�����ݴ˼��ɵõ�����a�IJ���ʽ�����a��ֵ�����ǵ��������Σ���������ۣ��ⷽ�̼������a��ֵ��
��� �⣺��1����S��AOC��S��BOC=1��3��
�⣺��1����S��AOC��S��BOC=1��3��
��OA��OB=1��3��
��-3x1=3x��
�������ߵĶԳ���Ϊֱ��x=1����
=1��
��x1=-1��x2=3��
�������ߵĽ���ʽ�ǣ�y=a��x+1����x-3������y=ax2-2ax-3a��
��2���ڽ���ʽy=-x-3�У���x=0����ã�y=3��
��C�������ǣ�0��-3����
�������ߵĽ���ʽy=ax2-2ax-3a��-3a=-3��
��a=1��
����κ����Ľ���ʽ�ǣ�y=x2-2x-3��
��OB=OC=3�����OBC�ǵ���ֱ�������Σ�
���AMC=90�㣬
���AMC�ǵ���ֱ�������Σ�
AC=
=
=
��
��뾶MA=MC=
��
=
��
��S����AMC=
=
�У�
��M��MD��x���ڵ�D����OD=1��AD=OA+DO=2��
��MD=
=1��
��M�������ǣ�1��-1����
��F��FE��x����E��
��M��AF���е㣮
��FE=2MD=2��AE=2AD=4��
��OE=3��
��F�������ǣ�3��-2����
ֱ��AF��б���ǣ�-
��
���F���ֱ�ߵ�б����2��
��������ʽ�ǣ�y+2=2��x-3������y=2x-8��
��3���ڣ�1���������£�AB=4��OC=3a��
��AC2=1+9a2��BC2=9+9a2��AB2=16��
����ABC�Ƕ۽�������ʱ��AC2+BC2��AB2ʱ��1+9a2+9+9a2��16��
��ã�0��a��
��
AC2+AB2��BC2ʱ��1+9a2+16��9+9a2���⣻
��BC2+AB2��AC2ʱ��9+9a2+16��1+9a2���⣮
�ʵ�0��a��
ʱ����ABC�Ƕ۽������Σ�
����ABC�ǵ���������ʱ����AC=AB����1+9a2=16����ã�a=
��
��BC=ABʱ��9+9a2=16����ã�a=
��
�ʵ�a=
��
ʱ����ABC�ǵ��������Σ�
 �⣺��1����S��AOC��S��BOC=1��3��
�⣺��1����S��AOC��S��BOC=1��3����OA��OB=1��3��
��-3x1=3x��
�������ߵĶԳ���Ϊֱ��x=1����
| x1+x2 |
| 2 |
��x1=-1��x2=3��
�������ߵĽ���ʽ�ǣ�y=a��x+1����x-3������y=ax2-2ax-3a��
��2���ڽ���ʽy=-x-3�У���x=0����ã�y=3��
��C�������ǣ�0��-3����
�������ߵĽ���ʽy=ax2-2ax-3a��-3a=-3��
��a=1��
����κ����Ľ���ʽ�ǣ�y=x2-2x-3��
��OB=OC=3�����OBC�ǵ���ֱ�������Σ�
���AMC=90�㣬
���AMC�ǵ���ֱ�������Σ�
AC=
| OA2+OC2 |
| 1+3 |
| 10 |
��뾶MA=MC=
| ||
| 2 |
| 10 |
| 5 |
��S����AMC=
90�С�(
| ||
| 360 |
| 5 |
| 4 |
��M��MD��x���ڵ�D����OD=1��AD=OA+DO=2��
��MD=
| MA2-AD2 |
��M�������ǣ�1��-1����
��F��FE��x����E��
��M��AF���е㣮
��FE=2MD=2��AE=2AD=4��
��OE=3��
��F�������ǣ�3��-2����
ֱ��AF��б���ǣ�-
| 1 |
| 2 |

���F���ֱ�ߵ�б����2��
��������ʽ�ǣ�y+2=2��x-3������y=2x-8��
��3���ڣ�1���������£�AB=4��OC=3a��
��AC2=1+9a2��BC2=9+9a2��AB2=16��
����ABC�Ƕ۽�������ʱ��AC2+BC2��AB2ʱ��1+9a2+9+9a2��16��
��ã�0��a��
| ||
| 3 |
AC2+AB2��BC2ʱ��1+9a2+16��9+9a2���⣻
��BC2+AB2��AC2ʱ��9+9a2+16��1+9a2���⣮
�ʵ�0��a��
| ||
| 3 |
����ABC�ǵ���������ʱ����AC=AB����1+9a2=16����ã�a=
| ||
| 3 |
��BC=ABʱ��9+9a2=16����ã�a=
| ||
| 3 |
�ʵ�a=
| ||
| 3 |
| ||
| 3 |
������������Ҫ�����˶��κ�����Բ�����κ�����һ�κ���֮����ۺ�Ӧ�ã��ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
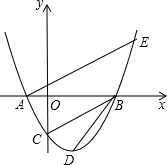 ACB=90�ȣ�
ACB=90�ȣ�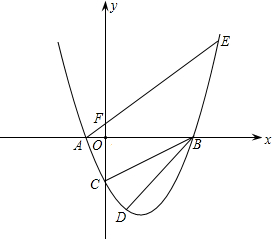 ��0������y�ύ�ڵ�C��0��-2�����ҡ�ACB=90�ȣ�
��0������y�ύ�ڵ�C��0��-2�����ҡ�ACB=90�ȣ�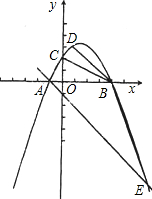 ��������y=ax2+bx+c��x�ύ��������ͬ�ĵ�A��-l��0����B��4��0������y�ύ�ڵ�C��0��2����
��������y=ax2+bx+c��x�ύ��������ͬ�ĵ�A��-l��0����B��4��0������y�ύ�ڵ�C��0��2���� m2-mb+n�������� a��b��c��m��nΪʵ������a��m��Ϊ0��
m2-mb+n�������� a��b��c��m��nΪʵ������a��m��Ϊ0��