题目内容
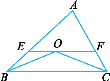
【题目】如图所示,点C为线段OB的中点,D为线段OA上一点.连结AC、BD交于点P.
(问题引入)(1)如图1,若点P为AC的中点,求![]() 的值.
的值.
温馨提示:过点C作CE∥AO交BD于点E.
(探索研究)(2)如图2,点D为OA上的任意一点(不与点A、O重合),求证:![]() .
.
(问题解决)(3)如图2,若AO=BO,AO⊥BO,![]() ,求tan∠BPC的值.
,求tan∠BPC的值.

【答案】(1)![]() ;(2) 见解析;(3)
;(2) 见解析;(3) ![]()
【解析】
(1)过点C作CE∥OA交BD于点E,即可得△BCE∽△BOD,根据相似三角形的性质可得![]() ,再证明△ECP≌△DAP,由此即可求得
,再证明△ECP≌△DAP,由此即可求得![]() 的值;(2)过点D作DF∥BO交AC于点F,即可得
的值;(2)过点D作DF∥BO交AC于点F,即可得![]() ,
,![]() ,由点C为OB的中点可得BC=OC,即可证得
,由点C为OB的中点可得BC=OC,即可证得![]() ;(3)由(2)可知
;(3)由(2)可知![]() =
=![]() ,设AD=t,则BO=AO=4t,OD=3t,根据勾股定理求得BD=5t,即可得PD=t,PB=4t,所以PD=AD,从而得∠A=∠APD=∠BPC,所以tan∠BPC=tan∠A=
,设AD=t,则BO=AO=4t,OD=3t,根据勾股定理求得BD=5t,即可得PD=t,PB=4t,所以PD=AD,从而得∠A=∠APD=∠BPC,所以tan∠BPC=tan∠A=![]() .
.
(1)如图1,过点C作CE∥OA交BD于点E,

∴△BCE∽△BOD,
∴![]() =
=![]() ,
,
又BC=![]() BO,∴CE=
BO,∴CE=![]() DO.
DO.
∵CE∥OA,∴∠ECP=∠DAP,
又∠EPC=∠DPA,PA=PC,
∴△ECP≌△DAP,
∴AD=CE=![]() DO,
DO,
即 ![]() =
=![]() ;
;
(2)如图2,过点D作DF∥BO交AC于点F,

则 ![]() =
=![]() ,
,![]() =
=![]() .
.
∵点C为OB的中点,
∴BC=OC,
∴![]() =
=![]() ;
;
(3)如图2,∵![]() =
=![]() ,
,
由(2)可知![]() =
=![]() =
=![]() .
.
设AD=t,则BO=AO=4t,OD=3t,
∵AO⊥BO,即∠AOB=90°,
∴BD=![]() =5t,
=5t,
∴PD=t,PB=4t,
∴PD=AD,
∴∠A=∠APD=∠BPC,
则tan∠BPC=tan∠A=![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n=400时,绿豆发芽的频率为0.955,所以绿豆发芽的概率是0.955;
②根据上表,估计绿豆发芽的概率是0.95;
③若n为4000,估计绿豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ① B. ①② C. ①③ D. ②③
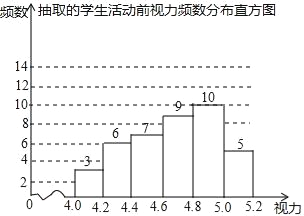
【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 3 |
4.4≤x<4.6 | 5 |
4.6≤x<4.8 | 8 |
4.8≤x<5.0 | 17 |
5.0≤x<5.2 | 5 |
(1)求活动所抽取的学生人数;
(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.