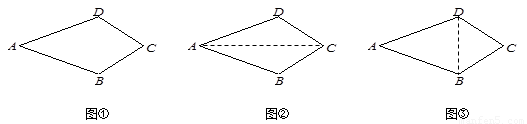题目内容
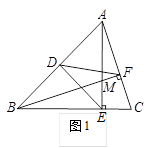
1.问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=![]() DF,则
DF,则![]() 的值为_____.
的值为_____.
2.拓展
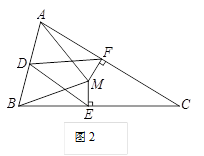
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
3.推广
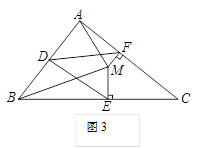
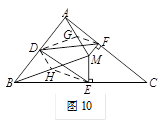
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
1.![]() 的值为 1
的值为 1
2.证明:如图9.

∵CB=CA,
∴∠CAB=∠CBA.
∵∠MAC=∠MBC,
∴∠CAB-∠MAC=∠CBA-∠MBC,
即∠MAB=∠MBA.
∴MA=MB.
∵ME⊥BC,MF⊥AC,垂足分别为点E,F,
∴∠AFM=∠BEM=90°.
在△AFM与△BEM中,
![]() ∠AFM=∠BEM,
∠AFM=∠BEM,
∠MAF =∠MBE,
MA=MB,
∴△AFM≌△BEM.
∵点D是AB边的中点,
∴BD = AD.
在△BDE与△ADF中,
![]() BD = AD,
BD = AD,
∠DBE =∠DAF,
BE = AF,
∴△BDE≌△ADF.
∴DE=DF.
3.解:DE=DF.
证明:分别取AM,BM的中点G,H,连接DG,FG,DH,EH.(如图10)
∵点D,G,H分别是AB,AM,BM的中点,
∴DG∥BM,DH∥AM,且DG=![]() BM,DH=
BM,DH=![]() AM.
AM.
∴四边形DHMG是平行四边形.
∴∠DHM =∠DGM,
∵ME⊥BC,MF⊥AC,垂足分别为点E,F,
∴∠AFM=∠BEM=90°.
∴FG=![]() AM=AG,EH=
AM=AG,EH=![]() BM=BH.
BM=BH.
∴FG= DH,DG= EH, ∠GAF=∠GFA,∠HBE =∠HEB.
∴∠FGM =2∠FAM,∠EHM =2∠EBM.
∵∠FAM=∠EBM,
∴∠FGM =∠EHM.
∴∠DGM+∠FGM =∠DHM+∠EHM,即∠DGF=∠DHE.
在△EHD与△DGF中,
![]() EH = DG,
EH = DG,
∠EHD =∠DGF,
HD = GF,
∴△EHD≌△DGF.
∴DE=DF.
解析:略

 阅读快车系列答案
阅读快车系列答案 |
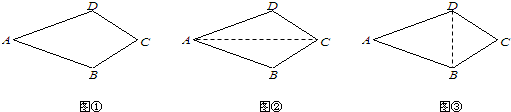
(1)文文同学证明过程如下:连结AC(如图②)
∵∠B=∠D ,AB=AD,AC=AC
∴△ABC≌△ADC,∴CB=CD
你认为文文的证法是 的.(在横线上填写“正确”或“错误”)
(2)彬彬同学的辅助线作法是“连结BD”(如图③),请完成彬彬同学的证明过程.
 为等腰直角三角形
为等腰直角三角形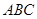 的重心,
的重心, ,直线
,直线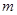 过点
过点 三点分别作直线
三点分别作直线 .
. 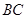 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段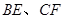 和
和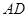 三者之间的数量关系并证明;
三者之间的数量关系并证明; 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.