题目内容
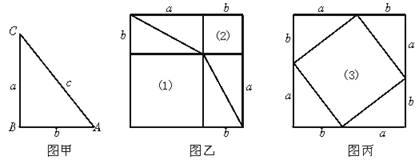
直角的两条直角边长AC,BC分别为6和8,∠C=90°,若把斜边AB绕点A旋转后,B点落在CA所在的直线上的点D处,那么∠BDC的正切值为 .
【答案】分析:先根据勾股定理求出AB的长,再根据旋转不变性,AB=AD.根据三角函数的定义可得tan∠BDC的值.
解答:解:由题知,AC,BC分别为6和8,∠C=90°,
∴AB= =
= =10,
=10,
①D点在AC的延长线上,CD=10-6=4,
∴tan∠BDC= =
= =2;
=2;
②D点在CA的延长线上,CD=10+6=16,
∴tan∠BDC= =
= =
= .
.
故答案为:2或 .
.
点评:本题主要考查三点:一是勾股定理;二是三角函数的定义;三是旋转图形的性质.注意分情况讨论.
解答:解:由题知,AC,BC分别为6和8,∠C=90°,
∴AB=
 =
= =10,
=10,①D点在AC的延长线上,CD=10-6=4,
∴tan∠BDC=
 =
= =2;
=2;②D点在CA的延长线上,CD=10+6=16,
∴tan∠BDC=
 =
= =
= .
.故答案为:2或
 .
.点评:本题主要考查三点:一是勾股定理;二是三角函数的定义;三是旋转图形的性质.注意分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目