题目内容
 如图,在⊙O中,已知∠BOD=100°,C是圆周上的一点,则∠BCD为
如图,在⊙O中,已知∠BOD=100°,C是圆周上的一点,则∠BCD为
- A.130°
- B.100°
- C.80°
- D.50°
A
分析:由在⊙O中,∠BOD=100°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BAD的度数,又由圆的内接四边形的性质,求得∠BCD的度数.
解答:∵∠BOD=100°,
∴∠BAD= ∠BOD=50°,
∠BOD=50°,
∵∠BAD+∠BCD=180°,
∴∠BCD=180°-∠BAD=130°.
故选A.
点评:此题考查了圆周角定理与圆的内接四边形的性质.此题难度不大,注意在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与圆的内接四边形对角互补定理的应用.
分析:由在⊙O中,∠BOD=100°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BAD的度数,又由圆的内接四边形的性质,求得∠BCD的度数.
解答:∵∠BOD=100°,
∴∠BAD=
 ∠BOD=50°,
∠BOD=50°,∵∠BAD+∠BCD=180°,
∴∠BCD=180°-∠BAD=130°.
故选A.
点评:此题考查了圆周角定理与圆的内接四边形的性质.此题难度不大,注意在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与圆的内接四边形对角互补定理的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,在△ABC中,已知B(-3,1).
22、如图,在△ABC中,已知B(-3,1). 9、如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点D,过D点作EF∥BC,交AB于点E,交AC于点F,若BE+CF=9,则线段EF的长为( )
9、如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点D,过D点作EF∥BC,交AB于点E,交AC于点F,若BE+CF=9,则线段EF的长为( ) 17、如图,在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是
17、如图,在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是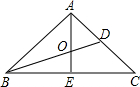 如图,在△ABC中,已知AB=AC=10,BC=16,O是△ABC的重心,则tan∠DBC的值是
如图,在△ABC中,已知AB=AC=10,BC=16,O是△ABC的重心,则tan∠DBC的值是 如图,在△ABC中,已知AB=AC,D为AB上一点,且AD=CD=BC,则∠B=
如图,在△ABC中,已知AB=AC,D为AB上一点,且AD=CD=BC,则∠B=