Question

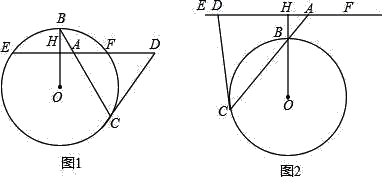
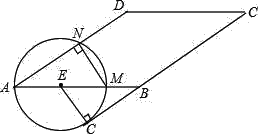
【题目】如图，在ABCD（AB＞AD）中，点E在边AB上，以点E为圆心，AE长为半径的⊙E分别交AB、AD于点N、N，与BC所在的直线相切于点G

（1）求证：EG∥MN；

（2）若AB=10，AD与BC之间的距离为6，求⊙E的半径．

Answer 1

【答案】(1)见解析;（2）⊙E的半径为．

【解析】

（1）根据平行四边形的性质可知∠1=∠2，根据直径所对的圆周角是直角可知∠ANM=90°，根据切线的性质可知∠BGE=90°，根据等角的余角相等可知∠3=∠4，即可证明EG∥MN；

（2）作AH⊥CG延长线于H，易证△BEG∽△BAH，根据对应边成比例得到BE与AE的数量关系，根据AE+EB=AB列方程求出AE即可．

如图所示，

∵四边形ABCD是平行四边形，

∴∠1=∠2，

∵AM是⊙E的直径，

∴∠ANM=90°，

∵BC所在的直线与⊙E相切于点G，

∴∠BGE=90°，

∴∠3=∠4，

∴EG∥MN；

（2）作AH⊥CG延长线于H，

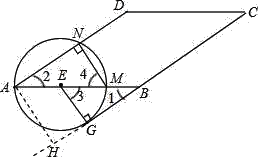
∵∠BGE=90°，

∴△BEG∽△BAH，

∴，

∵AE=GE，

∴，

∵AB=10，AH=6，

∴，

∴BE=AE，

∵AE+EB=AB，

∴AE+AE=10，

解得：AE=，

∴⊙E的半径为．