��Ŀ����
����Ŀ���ڳ��нεĺ���ѧϰ�У����Ǿ�������ȷ�������ı���ʽ�������ú���ͼ���о�������һһ���ú��������������ѧϰ���̣��ڻ�����ͼ��ʱ������ͨ������ƽ�Ƶķ�����������ѧ�ĺ���ͼ��ͬʱ������Ҳѧϰ�˾���ֵ������ ��
��
������澭����ѧϰ���̣�������������������:�ں���![]() �У���
�У���![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]() ����������ı���ʽ��
����������ı���ʽ��
![]() �ڸ�����ƽ��ֱ������ϵ�У�������ϲ���ķ����������������ͼ��
�ڸ�����ƽ��ֱ������ϵ�У�������ϲ���ķ����������������ͼ��
![]() ��֪����
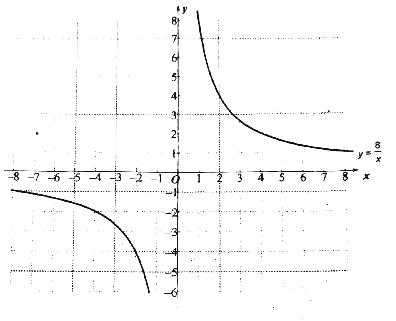
��֪����![]() ��ͼ����ͼ��ʾ������������ĺ���ͼ��ֱ��д������ʽ
��ͼ����ͼ��ʾ������������ĺ���ͼ��ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
���𰸡�![]()
![]() ��
�� ![]() ���������
���������![]()
![]() ��
��![]()
��������
��1����x=0��y=4��x=1��y=3���뺯��![]() �У����k��b���ɣ�
�У����k��b���ɣ�
��2�����ݣ�1���еı���ʽ���Ի����ú�����ͼ��
��3������ͼ�����ֱ��д������ʽ�Ľ⼯��
��1����x=0��y=4����![]() �ã�4=
�ã�4=![]() ��
��
��b=3��
��x=1��y=3��b=3����![]() �ã�
�ã�![]() ��
��
��k=1��
�������ı���ʽΪ![]() ��
��
��2��������ã�![]() ��
��
��ͼ������ͼ��

��3��������ͼ��ɵã���x<0��x![]() 2ʱ��
2ʱ��![]() ��
��
�ʴ�Ϊ��x<0��x![]() 2��
2��

��ϰ��ϵ�д�
�����Ŀ