题目内容
 如图所示,AB=12cm,AC=13cm,BD=4cm,DC=3cm,则该图形的面积为
如图所示,AB=12cm,AC=13cm,BD=4cm,DC=3cm,则该图形的面积为分析:先连接BC,根据勾股定理可求BC,易求BC2+AB2=AC2,从而利用勾股定理的逆定理可证△ABC是Rt△,再利用S四边形=S△ABC-S△BCD可求图形面积.
解答: 解:连接BC,如右图所示,
解:连接BC,如右图所示,
∵∠BDC=90°,BD=4,CD=3,
∴BC=
=5,
又∵52+122=169=132,
∴△ABC是直角三角形,
∴S四边形=S△ABC-S△BCD=
×AB×AC-
×BD×CD=
×12×5-
×3×4=24.
故答案是24.
 解:连接BC,如右图所示,
解:连接BC,如右图所示,∵∠BDC=90°,BD=4,CD=3,
∴BC=
| 32+42 |
又∵52+122=169=132,
∴△ABC是直角三角形,
∴S四边形=S△ABC-S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案是24.
点评:本题考查勾股定理、勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
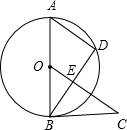 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.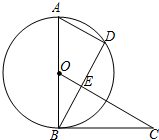 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
 。
。
