Question

【题目】如图，、是的两条半径，，点在上，与交于点，点在的延长线上，且.

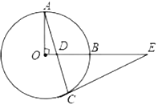
（1）求证：是的切线;

（2）当，时，直接写出的长.

Answer 1

【答案】（1）见解析；（2）CD=.

【解析】

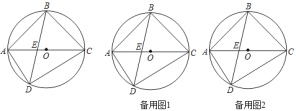
（1）连接OC，利用等边对等角和直角三角形的两锐角互余证得OC⊥CE即可得出结论；

（2）在Rt△AOD中求得∠ADO=90°，进而得出∠EDC=90°，根据等边三角形的判定可得△ECD是等边三角形，得出∠E=60°，然后在Rt△OCE中利用三角函数求出CE的长，即可得出CD的长．

（1）证明：连接OC.

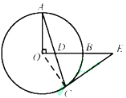
∵OA=OC,

∴∠A=∠OCD.

∵OA⊥OB,

∴∠AOB=90°.

∴∠A+∠ADO=90°.

∵CE=DE,

∴∠EDC=∠ECD=∠ADO.

∴∠OCD+∠ECD=90°.

∴OC⊥CE.

∵点C在⊙O上,

∴CE是⊙O的切线.

（2）解：∵OA⊥OB，

∴∠AOB=90°，

∴∠ADO=90°-∠A=90°-30°=60°，

∴∠EDC=∠ADO=60°，

∵CE=DE，

∴△ECD是等边三角形，

∴CD=CE，∠E=60°．

在Rt△OCE中，

CE===．

∴CD=CE=．