题目内容
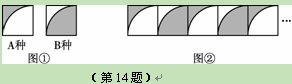
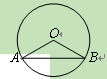
一条公路弯道处是一段圆弧
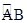，点O是这条弧所在圆的圆心，点C是的中点，OC与AB相交于点D。已知AB=120m，CD=20m，那么这段弯道的半径为（ ）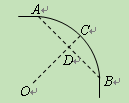
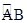，点O是这条弧所在圆的圆心，点C是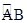的中点，OC与AB相交于点D。已知AB=120m，CD=20m，那么这段弯道的半径为（ ）C
分析：连接OA，由垂径定理求出AD的长，判断出△AOD的形状，在设OA=r，利用勾股定理即可得出r的长．
解答：解：连接OA，
∵C是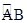的中点，OC与AB相交于点D，
∴AB⊥OC，
∴AD=
AB=×120
=60m，
∴△AOD是直角三角形，
设OA=r，则OD=r-CD=OC-CD=r-20，
在Rt△AOD中，
OA2=AD2+OD2，即r2=602+（r-20）2，解得r=100m．
故选C．
解答：解：连接OA，
∵C是
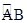的中点，OC与AB相交于点D，∴AB⊥OC，
∴AD=
AB=×120=60m，
∴△AOD是直角三角形，
设OA=r，则OD=r-CD=OC-CD=r-20，
在Rt△AOD中，
OA2=AD2+OD2，即r2=602+（r-20）2，解得r=100m．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
、
、
在⊙O上，若
，则
的度数为 ( ).
，AB=3，弦BC∥OA，则劣弧BC的弧长为（ ）
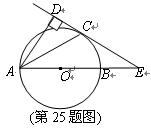
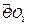和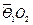
，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧
?
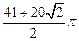