Question

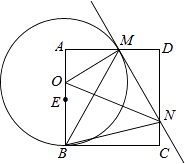
【题目】如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．下列结论：①CE=CF；②线段EF的最小值为2 ；③当AD=2时，EF与半圆相切；④若点F恰好落在 上，则AD=2 ；⑤当点D从点A运动到点B时，线段EF扫过的面积是16 ．其中正确结论的序号是 ．

Answer 1

【答案】①、③、⑤
【解析】解：①连接CD，如图1所示．
∵点E与点D关于AC对称，
∴CE=CD．
∴∠E=∠CDE．
∵DF⊥DE，
∴∠EDF=90°．
∴∠E+∠F=90°，∠CDE+∠CDF=90°．
∴∠F=∠CDF．
∴CD=CF．
∴CE=CD=CF．
∴结论“CE=CF”正确．
②当CD⊥AB时，如图2所示．

∵AB是半圆的直径，
∴∠ACB=90°．
∵AB=8，∠CBA=30°，
∴∠CAB=60°，AC=4，BC=4 ．
∵CD⊥AB，∠CBA=30°，
∴CD= BC=2 ．
根据“点到直线之间，垂线段最短”可得：
点D在线段AB上运动时，CD的最小值为2 ．
∵CE=CD=CF，
∴EF=2CD．
∴线段EF的最小值为4 ．
∴结论“线段EF的最小值为2 ”错误．
③当AD=2时，连接OC，如图3所示．

∵OA=OC，∠CAB=60°，
∴△OAC是等边三角形．
∴CA=CO，∠ACO=60°．
∵AO=4，AD=2，
∴DO=2．
∴AD=DO．
∴∠ACD=∠OCD=30°．
∵点E与点D关于AC对称，
∴∠ECA=∠DCA．
∴∠ECA=30°．
∴∠ECO=90°．
∴OC⊥EF．
∵EF经过半径OC的外端，且OC⊥EF，
∴EF与半圆相切．
∴结论“EF与半圆相切”正确．
④当点F恰好落在 上时，连接FB、AF，如图4所示．

∵点E与点D关于AC对称，
∴ED⊥AC．
∴∠AGD=90°．
∴∠AGD=∠ACB．
∴ED∥BC．
∴△FHC∽△FDE．
∴ ．
∵FC= EF，
∴FH= FD．
∴FH=DH．
∵DE∥BC，
∴∠FHC=∠FDE=90°．
∴BF=BD．
∴∠FBH=∠DBH=30°．
∴∠FBD=60°．
∵AB是半圆的直径，
∴∠AFB=90°．
∴∠FAB=30°．
∴FB= AB=4．
∴DB=4．
∴AD=AB﹣DB=4．
∴结论“AD=2 ”错误．
⑤∵点D与点E关于AC对称，

点D与点F关于BC对称，
∴当点D从点A运动到点B时，
点E的运动路径AM与AB关于AC对称，
点F的运动路径NB与AB关于BC对称．
∴EF扫过的图形就是图5中阴影部分．
∴S阴影=2S△ABC
=2× ACBC
=ACBC
=4×4
=16 ．
∴EF扫过的面积为16 ．
∴结论“EF扫过的面积为16 ”正确．
所以答案是：①、③、⑤．
【考点精析】本题主要考查了垂线段最短和平行线的判定与性质的相关知识点，需要掌握连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用；由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质才能正确解答此题．