题目内容
在△ABC中,若∠ACB=120°,AC=BC,AB边上的高CD=3,则AC=________,AB=________,BC边上的高AE=________.
6 

分析:根据等腰三角形的性质AD=BD、∠CAB=∠CBA=30°.在Rt△ACD中,利用“30°角所对的直角边是斜边的一半”求得AC=6,进而由勾股定理求得AD的长度;最后由三角形的面积公式来求AE的长度.
解答: 解:∵在△ABC中,若∠ACB=120°,AC=BC,
解:∵在△ABC中,若∠ACB=120°,AC=BC,
∴∠CAB=∠CBA=30°.
又∵CD⊥AB,
∴AC=2CD=6(30°角所对的直角边是斜边的一半),AD=BD.
在Rt△ACD中,AD= =
= =3
=3 .
.
则AB=2AD=6 .
.
∵S△ABC= AB•CD=
AB•CD= BC•AE,
BC•AE,
∴AE=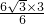 =3
=3 .
.
故答案分别是:6;6 ;3
;3 .
.
点评:本题考查了勾股定理,等腰三角形的性质.注意,边BC上的高线应该是交BC的延长线于点E.


分析:根据等腰三角形的性质AD=BD、∠CAB=∠CBA=30°.在Rt△ACD中,利用“30°角所对的直角边是斜边的一半”求得AC=6,进而由勾股定理求得AD的长度;最后由三角形的面积公式来求AE的长度.
解答:
 解:∵在△ABC中,若∠ACB=120°,AC=BC,
解:∵在△ABC中,若∠ACB=120°,AC=BC,∴∠CAB=∠CBA=30°.
又∵CD⊥AB,
∴AC=2CD=6(30°角所对的直角边是斜边的一半),AD=BD.
在Rt△ACD中,AD=
 =
= =3
=3 .
.则AB=2AD=6
 .
.∵S△ABC=
 AB•CD=
AB•CD= BC•AE,
BC•AE,∴AE=
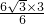 =3
=3 .
.故答案分别是:6;6
 ;3
;3 .
.点评:本题考查了勾股定理,等腰三角形的性质.注意,边BC上的高线应该是交BC的延长线于点E.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为( )
如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为( )