题目内容
(11·大连)(本题12分)在△ABC中,∠A=90°,点D在线段BC上,∠EDB=
 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.(1)当AB=AC时,(如图13),
① ∠EBF=_______°;
② 探究线段BE与FD的数量关系,并加以证明;
(2)当AB=kAC时(如图14),求
 的值(用含k的式子表示).
的值(用含k的式子表示).

解:(1)①22.5°…………………………2分

证明:如图1,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H

则∠GDB=∠C ∠BHD=∠A=90°=∠GHB

又∵DE=DE,∠DEB=∠DEG=90°
∴△DEB≌△DEG

∵AB=AC ∠A=90°
∴∠ABC=∠C=∠GDB
∴HB=HD
∵∠DEB=∠BHD=90° ∠BFE=∠DFH
∴∠EBF=∠HDF
∴△GBH≌△FDH
∴GB=FD…………………………6分

(2)如图1,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H

 又∵DG∥CA
又∵DG∥CA
∴△BHD∽△BAC

第二种解法:
解:(1)①∵AB=AC∠A=90°
∴∠ABC=∠C=45°
∵∠EDB= ∠C
∠C
∴∠EDB=22.5°
∵BE⊥DE
∴∠EBD=67.5°
∴∠EBF=67.5°-45°=22.5°
②在△BEF和△DEB中
∵∠E=∠E=90°
∠EBF=∠EDB=22.5°
∴△BEF∽△DEB
如图:BG平分∠ABC,

∴BG=GD△BEG是等腰直角三角形
设EF=x,BE=y,
则:BG=GD= y
y
FD= y+y-x
y+y-x
∵△BEF∽△DEB
∴ =
=
即: =
=
得:x=( -1)y
-1)y
∴FD= y+y-(
y+y-( -1)y=2y
-1)y=2y
∴FD=2BE.
(2)如图:作∠ACB的平分线CG,交AB于点G,

∵AB=kAC
∴设AC=b,AB=kb,BC= b
b
利用角平分线的性质有: =
=
即: =
=
得:AG=
∵∠EDB= ∠ACB
∠ACB
∴tan∠EDB=tan∠ACG=
∵∠EDB= ∠ACB
∠ACB
∠ABC=90°-∠ACB
∴∠EBF=90°-∠ABC-∠EDB= ∠ACB
∠ACB
∴△BEF∽△DEB
∴EF= BE
BE
ED= BE=EF+FD
BE=EF+FD
∴FD= BE-
BE- BE=
BE= BE.
BE.
∴ =
= .解析:
.解析:
略

证明:如图1,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H

则∠GDB=∠C ∠BHD=∠A=90°=∠GHB

又∵DE=DE,∠DEB=∠DEG=90°
∴△DEB≌△DEG

∵AB=AC ∠A=90°
∴∠ABC=∠C=∠GDB
∴HB=HD
∵∠DEB=∠BHD=90° ∠BFE=∠DFH
∴∠EBF=∠HDF
∴△GBH≌△FDH
∴GB=FD…………………………6分

(2)如图1,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H

 又∵DG∥CA
又∵DG∥CA∴△BHD∽△BAC

第二种解法:
解:(1)①∵AB=AC∠A=90°
∴∠ABC=∠C=45°
∵∠EDB=
 ∠C
∠C∴∠EDB=22.5°
∵BE⊥DE
∴∠EBD=67.5°
∴∠EBF=67.5°-45°=22.5°
②在△BEF和△DEB中
∵∠E=∠E=90°
∠EBF=∠EDB=22.5°
∴△BEF∽△DEB
如图:BG平分∠ABC,

∴BG=GD△BEG是等腰直角三角形
设EF=x,BE=y,
则:BG=GD=
 y
yFD=
 y+y-x
y+y-x∵△BEF∽△DEB
∴
 =
=
即:
 =
=
得:x=(
 -1)y
-1)y∴FD=
 y+y-(
y+y-( -1)y=2y
-1)y=2y∴FD=2BE.
(2)如图:作∠ACB的平分线CG,交AB于点G,

∵AB=kAC
∴设AC=b,AB=kb,BC=
 b
b利用角平分线的性质有:
 =
=
即:
 =
=
得:AG=

∵∠EDB=
 ∠ACB
∠ACB∴tan∠EDB=tan∠ACG=

∵∠EDB=
 ∠ACB
∠ACB ∠ABC=90°-∠ACB
∴∠EBF=90°-∠ABC-∠EDB=
 ∠ACB
∠ACB∴△BEF∽△DEB
∴EF=
 BE
BEED=
 BE=EF+FD
BE=EF+FD∴FD=
 BE-
BE- BE=
BE= BE.
BE.∴
 =
= .解析:
.解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
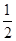 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.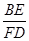 的值(用含k的式子表示).
的值(用含k的式子表示).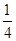 (容器各面的厚
(容器各面的厚