Question

已知△ABC的∠B、∠C的平分线交于O，∠BOC=100°，则∠A=________．

Answer 1

20°
分析：由于BE、CD是∠B、∠C的角平分线，易得∠ABE=∠CBE，∠ACD=∠BCD，从而有∠ABE+∠ACD=∠CBE+∠BCD，利用外角的性质可得∠BOC=∠BDO+∠ABE，∠BDO=∠A+∠ACD，易求∠BOC=∠A+∠ACD+∠ABE，再利用三角形内角和可得∠CBE+∠BCD=180°-∠BOC，再代入∠BOC=∠A+∠ACD+∠ABE中，易求∠A．
解答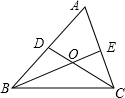：解：如右图所示，
∵BE、CD是∠B、∠C的角平分线，
∴∠ABE=∠CBE，∠ACD=∠BCD，
∴∠ABE+∠ACD=∠CBE+∠BCD，
∵∠BOC=∠BDO+∠ABE，∠BDO=∠A+∠ACD，
∴∠BOC=∠A+∠ACD+∠ABE，
又∵∠BOC+∠CBE+∠BCD=180°，
∴∠CBE+∠BCD=180°-∠BOC，
∴∠BOC=180-∠BOC+∠A，
∴∠A=20°．
故答案是20°．
点评：解题的关键是联合运用三角形内角定理和三角形外角性质，注意等量代换．