题目内容
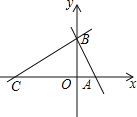
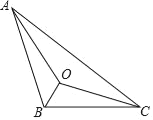
【题目】如图，O是△ABC内一点，∠OBC＝60°，∠AOC＝120°，OA＝OC＝
，OB＝1，则AB边的长为_____．
【答案】
【解析】
如图，将△AOB顺时针旋转120°直至OA与OC重合，于是得到∠BOB'＝120°，OB＝OB'＝1，根据等腰三角形的性质得到∠OBB'＝30°，推出∠B'BA＝90°，BB'＝
，过O作OD⊥BA，垂足为D，解直角三角形即可得到结论．
如图，将△AOB顺时针旋转120°直至OA与OC重合，则∠BOB'＝120°，OB＝OB'＝1，
∴∠OBB'＝30°，
∵∠OBC＝60°，
∴∠B'BA＝90°，BB'＝ ，
过O作OD⊥BA，垂足为D，
∵∠OBD＝60°，OB＝1，
∴BD＝
，OD＝
，
在Rt△ODC中，CD＝
，
∴BC＝BD+CD＝4，
在Rt△B'BA中，AB'＝
，
∴AB＝AB'＝，
故答案为：．
练习册系列答案
发散思维新课堂系列答案
相关题目
