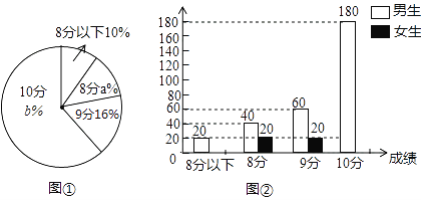
题目内容
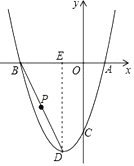
【题目】如图，已知抛物线y = x2 + bx + c的图象经过点A（l ，0） ，B（﹣3 ，0） ，与y轴交于点C ，抛物线的顶点为D ，对称轴与x轴相交于点E ，连接BD ．
（1）求抛物线的解析式 ．
（2）若点P在直线BD上，当PE = PC时，求点P的坐标 ．
（3）在（2）的条件下，作PF⊥x轴于F ，点M为x轴上一动点 ，N为直线PF上一动点 ，G为抛物线上一动点，当以点F ，N ，G ，M 四点为顶点的四边形为正方形时，求点M的坐标 ．
【答案】（1）y=x2+2x﹣3（2）（﹣2，﹣2）（3）（
，0），（
，0）
【解析】试题分析：（1）利用待定系数法即可得出结论；
（2）先确定出点E的坐标，利用待定系数法得出直线BD的解析式，利用PC=PE建立方程即可求出a即可得出结论；
（3）设出点D的坐标，进而得出点G，N的坐标，利用FM=MG建立方程求解即可得出结论．
试题解析：解：（1）∵抛物线
的图象经过点A（1，0），B（﹣3，0），∴
，∴
，∴抛物线的解析式为
；
（2）由（1）知，抛物线的解析式为
，∴C（0，﹣3），抛物线的顶点D（﹣1，﹣4），∴E（﹣1，0），设直线BD的解析式为y=mx+n，∴
，∴
，∴直线BD的解析式为y=﹣2x﹣6，设点P（a，﹣2a﹣6），∵C（0，﹣3），E（﹣1，0），根据勾股定理得，PE2=（a+1）2+（﹣2a﹣6）2，PC2=a2+（﹣2a﹣6+3）2，∵PC=PE，∴（a+1）2+（﹣2a﹣6）2=a2+（﹣2a﹣6+3）2，∴a=﹣2，∴y=﹣2×（﹣2）﹣6=﹣2，∴P（﹣2，﹣2）；
（3）如图，作PF⊥x轴于F，∴F（﹣2，0），设D（d，0），∴G（d，d2+2d﹣3），N（﹣2，d2+2d﹣3），∵以点F，N，G，M四点为顶点的四边形为正方形，必有FM=MG，∴|d+2|=|d2+2d﹣3|，∴d=
或d=
，∴点M的坐标为（
，0），（
，0），（
，0），（
，0）．
